1. BEVEZETÉS
A kisciklusú termomechanikai fáradás kinetikája a reaktortartály anyagában c. esettanulmány a Nagy teljesítőképességű szerkezeti anyagok kutatása c. TÁMOP (lásd a Láncmodell c. esettanulmány [14] hivakozását) project keretében végzett kutatómunka egyik fontos eredményét foglalja össze. A TÁMOP projekt szakmai vezetője Trampus Péter professzor volt, és ennek 11 altémája közül a nukleáris erőművek reaktortartály anyagával kapcsolatos kutatásokat vezette Fekete Balázs, aki ebből a témából szerezte meg a PhD fokozatot, és jelenleg egy USA-beli high tech vállalat fejlesztőmérnöke.
Az ebben az altémában végzett mechanikai, röntgendiffrakciós és TEM-es vizsgálatok értékelésekor vetődtek fel olyan kérdések, amelyek értelmezésébe engem is bevontak, nevezetesen a Cottrell-féle elmélet lehetséges alkalmazásával kapcsolatban. Ez az ötlet Fekete Balázs munkájában termékeny talajra talált. A TEM-es vizsgálatokat dr. Radnóczi György (KFKI MFA), míg az XRD vizsgálatokat Ungár Tamás professzor (ELTE Anyagfizika Tanszék) irányításával Jóni Bertalan (PhD) végezte. A Cottrell-féle elmélettel egyébként még a ’70-es évek közepén ismerkedtem meg a lágyacélok folyási jelenségének értelmezése során. Ezzel a kérdéssel majd egy következő esettanulmányban foglalkozom.
2. SZAKIRODALMI HÁTTÉR
2.1 KISCIKLUSÚ FÁRADÁS
A legtöbb gépészeti szerkezetünket úgy méretezzük, hogy annak anyagában a folyáshatár biztonsági tényezővel csökkentett értékénél nagyobb igénybevétel ne jöhessen létre. Ennek ellenére elkerülhetetlen olyan lokális feszültséggyűjtő helyek kialakulása, melyekben az előre nem ismert járulékos terhelések hatására bizonyos mértékű képlékeny alakváltozás lép fel. Ilyen helyek lehetnek például a hirtelen keresztmetszet változások, hegesztési varratok környezete, furatok, vagy a berendezés olyan részei, melyben bizonyos időtartamra olyan inhomogén hőmérsékletmező alakul ki, amely jelentős feszültséget okoz a szerkezet anyagában, és amellyel a méretezésnél nem számoltunk. Ha a kritikus helyeken a képlékeny alakváltozás csak egyszer jön létre, akkor annak mértékétől függően a feszültségmező átrendeződésével és a kritikus hely környezetében lévő nagy feszültség gradiens leépülésével az anyag teherbíró képessége növekedhet a képlékeny keményedés által [Lee et al., 2005]. Ha ezek a méretezés során elhanyagolt folyáshatár feletti igénybevételek többször megismétlődnek, az anyag mikroszerkezete az ismétlődő makroszkopikus képlékeny alakváltozás hatására megváltozik, benne repedések keletkezhetnek. Ez a folyamat végül a szerkezeti integritás megszűnéséhez, azaz repedésterjedéshez, majd töréshez vezet. A fent leírt jelenséget nevezi a szakirodalom kisciklusú fáradásnak.
2.2 MIKROSZERKEZETI VÁLTOZÁSOK A FÁRADÁSI FOLYAMAT SORÁN
A fáradási folyamat során az anyagban mikroszerkezeti változások mennek végbe, amelyek a mechanikai tulajdonságok megváltozásához és károsodáshoz vezetnek. Ez főként a diszlokációk és a pontszerű rácshibák mennyiségének és struktúrájának változását, illetve az egymással és a különböző fázisokkal lejátszódó reakcióit jelenti [Lukács, 2012]. A következőkben az erőművi acélokra vonatkozó eredményekre fókuszálva áttekintjük a kisciklusú fáradás során létrejövő mikroszerkezeti változásokkal kapcsolatos kutatásokat.
[Ginsztler, 1988] erőművi gőzfejlesztő acélok intenzív hőmérséklet ciklusok hatására létrejövő hőfáradásának mikroszerkezetre gyakorolt hatását vizsgálta. A hőciklusok hatására szubszemcsék képződését figyelte meg a diszlokációsűrűség növekedése mellett. Sankar és munkatársai nagy hőmérsékleten üzemelő berendezésekben használt 9Cr-1Mo ferrites acélon végeztek szinkron és aszinkron termomechanikus fárasztóvizsgálatot majd a tönkremenetelig végzett mérések mintáinak fémtani elemzésével vizsgálták a repedéskeletkezés mechanizmusát [Shankar, et al., 2012]. A TEM felvételeiken ekviaxiális szubszemcsék voltak láthatók a fárasztott mintákon. Kimutatták, hogy a szemcsehatárokon jelen lévő karbidok jelentős szerepet játszanak a mikrorepedések keletkezésében, melyek a szemcsehatár mentén terjednek. Mayer és munkatársai gőzturbinákban használt bainites szövetszerkezetű melegszilárd acélon végeztek megszakított fárasztási kísérleteket [Mayer et al., 2012]. A kísérleti anyag ciklikusan lágyuló viselkedést mutatott, a lágyulás mértéke jelentősen függött az alakváltozás sebességétől és a hőmérséklettől. A különböző halmozódó károsodást elszenvedett próbatesteken meghatározták a diszlokációsűrűséget röntgen vonalprofil analízissel és TEM felvételekből, valamint a szubszemcseméretet, melyből látható, hogy a diszlokációsűrűség csökkenő, míg a cellaméret növekvő tendenciát mutat a fáradási folyamat előrehaladásával. He és munkatársai fúziós reaktorokban alkalmazott melegszilárd acél fáradás alatti mechanikai tulajdonságainak és mikroszerkezetének kapcsolatát vizsgálták [He et al., 2014]. A kiindulási állapotú és a tönkremenetelig fárasztott minták diszlokációsűrűségét TEM felvételekből határozták meg, mely nem mutatott változást sem a ciklusszám növelésével, sem az alakváltozás amplitúdó változtatásával.
Ezen a területen végzett irodalomkutatásból megállapítható, hogy fáradási folyamat mikroszerkezeti vonatkozásaival kapcsolatban nincs egységesen elfogadott álláspont. Ezért helye van a mikroszerkezet további együttes kvalitatív (TEM, SEM) és kvantitatív (XRD) elemzésének, aminek eredményei a fáradás folyamán lejátszódó mikroszerkezeti változások jobb megértéséhez vezethetnek.
3. KÍSÉRLETI ANYAGOK, ALKALMAZOTT BERENDEZÉSEK ÉS ESZKÖZÖK
3.1 A VIZSGÁLT ACÉLOK TULAJDONSÁGAI
A 15H2MFA jelű reaktortartály acélt az MVM Paksi Atomerőmű Zrt. bocsátotta rendelkezésünkre, egy 149 × 110 × 305 mm méretű, Csehországban gyártott reaktortartály acélból származó tömb formájában. A kísérleti anyag beérkezését követően a próbatestek gyártásának megkezdése előtt átfogó állapotfelmérést végeztünk, amely az acélok fémtani vizsgálatából és a mechanikai tulajdonságaik méréséből állt. A kísérleti anyagok névleges, és optikai emissziós spektrométerrel meghatározott kémiai összetétele az 1. táblázatban látható. A kísérleti anyag összetétele megfelel a gyártó által megadott előírásoknak, az egyes elemeknél mért eltérés nem számottevő.
1. táblázat. A kísérleti anyag kémiai összetétele, tömeg%
| Anyag | C | Si | Mn | S | P | Cr | Ni | Mo | V | As | Co | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
15H2MFA | Névle- ges | 0,13-0,18 | 0,17-0,37 | 0,30-0,60 | max. 0,025 | max. 0,025 | 2,50-3,00 | max. 0,04 | 0,60-0,80 | 0,25-0,35 | max. 0,05 | max. 0,02 |
| Kísérl. anyag | 0,14 | 0,26 | 0,37 | 0,012 | 0,009 | 2,92 | 0,08 | 0,497 | 0,27 | – | – |
A beszállított acéltömbökből a hőkezeltségi állapot felderítése érdekében fénymikroszkópon szövetszerkezet vizsgálatokat és keménységmérést végeztünk, melyből megállapítottuk, hogy a reaktortartály acél a kovácsolást követő ferrit-perlites (normalizált) szövetszerkezetű volt. Emiatt a próbatestek hasáb alakú előgyártmányait az esztergálást megelőzően a tartály kovácsolt gyűrűinek gyári technológiai utasítása szerint hőkezeltük; 1000 °C-ról olajban edzettük, majd 15 órán át 680 °C-on megeresztettük. A 15H2MFA acél Cr, Mo, V ötvözésének hatására a ferrit-perlites átalakulás az acél folyamatos lehűtésre vonatkozó átalakulási diagramján oly mértékben jobbra tolódik, hogy a lehűtés után a reaktortartály 140–170 mm-es szelvényű fő elemeinél csak martenzit és bainit alakul ki, melyek aránya attól függ, hogy a vizsgált anyagrész milyen távolságban helyezkedik el a hűtőfolyadékkal közvetlenül érintkező felületektől. A hőkezelés hatására finomszerkezetű szemcsés bainit alakul ki, az igénybevétel hőmérsékletén termodinamikailag stabil, diszperz eloszlású Cr-Mo-V komplex karbidokkal [Davies, 1997; Gorynin, 1998]. Erre az acélra jellemző karbidszerkezet eltér a nyugati nyomottvizes reaktortartályok anyagáétól, mivel finomabb eloszlású, kisebb méretű és főként vanádiumban gazdag kiválásokat tartalmaz [Davies, 1997].
A hőkezelést követően a 15H2MFA acél szövetszerkezetéről készült fénymikroszkópos felvétel az 1. ábrán látható. A minták csiszolatain mikrokeménység méréseket is végeztünk egy Wilson Wolpert 401 MVD típusú mikrokeménység mérő berendezésen, 5 N terheléssel. A reaktortartály acél hőkezelés utáni keménysége HV0,5 230±5 értékre adódott.

A hőkezelést követően a hasáb előgyártmányok egy részéből arányos szakító próbatestet munkáltunk ki, melyeket kvázi-statikus szakítóvizsgálatnak vetettünk alá a következő alfejezetben ismertetett termomechanikus fárasztás szélső hőmérsékletein, melyek 150°C és 270°C. Az eredmények a 2. ábrán láthatóak melyekből megállapítható, hogy e két hőmérsékleten a mechanikai tulajdonságokban jelentős eltérés nem tapasztalható, és a kísérleti anyagok szilárdsági jellemzői a 2. táblázat szerinti gyártó által előírt értékeknek megfelelnek.
2. táblázat. A kísérleti anyagok gyártó által megadott mechanikai tulajdonságai
| 20 °C | 350 °C | |||||||
|---|---|---|---|---|---|---|---|---|
| Anyag | Rm [MPa] | Rp0,2 [MPa] | A40 [%] | Z [%] | Rm [MPa] | Rp0,2 [MPa] | A40 [%] | Z [%] |
| 15H2МFА | 540 | 431 | 14 | 50 | 490 | 392 | 13 | 50 |
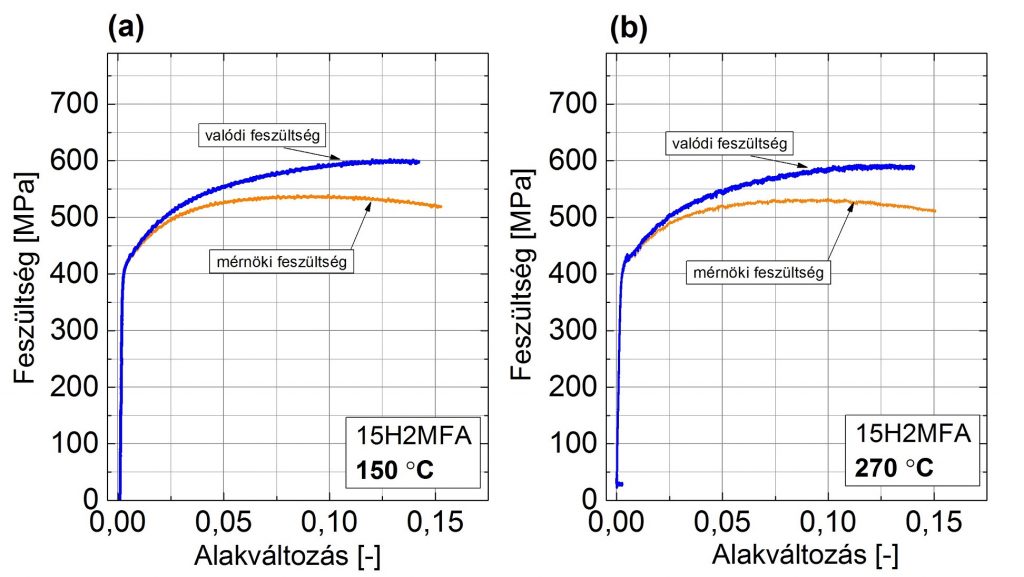
2. ábra. Szakítóvizsgálatok (a) 15H2MFA, T=150 °C (b) 15H2MFA, T=270 °C
3.2 A KÍSÉRLETEKHEZ ALKALMAZOTT BERENDEZÉS BEMUTATÁSA
A méréseket egy Gleeble 3800 típusú fizikai szimulátoron hajtottuk végre, amelynek átfogó képe a 3. ábrán látható. A berendezés egy többfunkciós szimulátor, amely különböző fémtechnológiai és fémtani folyamatok fizikai szimulációjára, fémes szerkezeti anyagok termomechanikus kezeléseire és anyagvizsgálatára egyaránt alkalmas [Bereczki et al., 2014].

3. ábra. A Gleeble 3800 termomechanikus fizikai szimulátor a fárasztóvizsgálatokhoz alkalmazott átalakító egységgel
4. A TERMOMECHANIKUS FÁRASZTÓKÍSÉRLETEK
4.1 A KÍSÉRLETI ELRENDEZÉS KIDOLGOZÁSA, VIZSGÁLATI PARAMÉTEREK

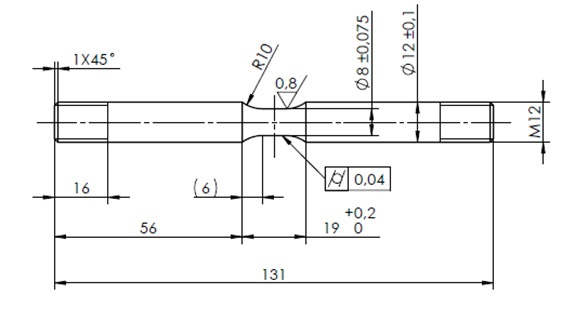
A próbatest végleges alakja a 4. ábrán látható. A próbatestek 13 mm élhosszúságú négyzet alapú hasáb előgyártmányokból, CNC esztergán készültek.
B. Próbatest befogása, felműszerezés
A 6. ábrán a vizsgálóberendezés kamraterét mutatjuk be a fárasztóvizsgálatokhoz előkészített állapotban. A húzó igénybevétel felvételét a próbatestek (1) végein kialakított M12 menethez kapcsolódó nagyméretű csavaranyák (2), a nyomó igénybevétellel szembeni megtámasztást a szorító kengyelek (3) biztosítják.

5. AZ ANYAGSZERKEZETBEN LEJÁTSZÓDÓ VÁLTOZÁS KINETIKÁJÁNAK VIZSGÁLATA
5.1 MEGSZAKÍTOTT FÁRASZTÓVIZSGÁLATOK
A 4. pontban leírt módon meghatároztuk a kísérleti anyagok adott fárasztási paraméterekhez tartozó élettartamát, mely eredményeket a megszakított fárasztási vizsgálatok tervezésénél használtuk fel. A terhelési szint kiválasztásánál, az üzemi körülményeket legjobban modellező igénybevétel definiálása volt a célunk, emiatt εa = 0,3%-ra választottuk megszakított fárasztókísérletek terhelés amplitúdóját.
3. táblázat. A megszakított fárasztóvizsgálatok paraméterei
| Mérés | Mechanikai nyúlás amplitúdó εa | Vizsgálati hőmérséklet T | Károsodási tényező UF = N/Nf | Ciklusszám N |
|---|---|---|---|---|
| 15H2MFA TMF | 0,3% | 150-270 °C | 0,05 | 106 |
| 15H2MFA TMF | 0,25 | 594 | ||
| 15H2MFA TMF | 0,50 | 1188 | ||
| 15H2MFA TMF | 0,70 | 1663 |
A 15H2MFA anyag terhelési szintjének meghatározásánál figyelembe vettük, hogy a nagyobb alakváltozás amplitúdó az anyag fáradási viselkedésének tanulmányozásához, és a fáradási modell felvételéhez szükséges, azonban a valós berendezésen a geometriai kényszerek miatt üzem közben nem jellemzőek ekkora alakváltozások. A kiválasztott terhelési szinteken a 15H2MFA anyag átlagos tönkremeneteli élettartama (Nf) 2376 ciklus, melyet négy részre osztottunk a 3. táblázat szerint.
5.2 MIKROSZERKEZETI VÁLTOZÁSOK A FÁRADÁS SORÁN
A 15H2MFA anyag mikroszerkezetéről hőkezelt, kiindulási állapotában készült TEM felvétel látható a 7.(a) ábrán, ahol a szemcsék belsejét 0,3-1 µm széles hosszúkás cellák tagolják. A felvételen látható 0,1-0,2 µm átmérőjű fekete szemcsék karbid kiválások, melyek többsége a cellahatárokon fekszik. Az átlagos diszlokációsűrűség nagy ebben az állapotban (0,7 × 1014 / m2), ami jellemző a bainites szerkezetre [Mayer et al., 2012]. A diszlokáció-szerkezet homogén eloszlást mutat. A legkisebb mértékű károsodást elszenvedett minta (7.(b) ábra) szemcséiben lévő cellák hasonló alakúak, irányuk szemcsénként változik.

A ciklikus terhelés hatására cellák mérete változatlan a kiindulási állapothoz képest, azonban az XRD mérések szerint az átlagos diszlokációsűrűség az 1,2 × 1014 / m2 értékre növekedett. A 0,25-os károsodás értéknél a cellák méretének kismértékű csökkenése figyelhető meg (8.(a) ábra), és ebben az állapotban mértük a legnagyobb diszlokációsűrűség értéket (6,1 × 1014 / m2). A legjelentősebb változást az élettartam felénél (UF = 0,50) megszakított minták mikroszerkezeténél tapasztaltuk (8.(b) ábra). Itt a korábbi állapotokhoz képest a cellák méretének határozott növekedése figyelhető meg, mialatt a diszlokációsűrűség jelentősen csökkent (3,2 × 1014 / m2). Megfigyelhető a cellafalak elhajlása, melyet vélhetően relaxációs folyamat eredményezett, melyből blokkolt diszlokáció-mozgásra következtethetünk.

A 70%-os károsodást elszenvedett minták vizsgálata során az előzőekben ismertetett folyamat szerinti változást tapasztaltunk, a cellaméret további növekedése és a diszlokációsűrűség csökkenése volt megfigyelhető (9.(a) ábra). A 9.(b) ábra jellemző diszlokációban szegény térképet mutat. Az elnyújtott diszlokációk jellemzően a karbid-kiválásokon vannak feltűzve. Meyer és munkatársai melegszilárd bainites, ciklikusan lágyuló acélon végzett hasonló kutatómunkájuk során a diszlokációsűrűség folyamatos csökkenését és a cellaméret növekedését regisztrálták [Mayer et al., 2012]. Fontos szempont, hogy a 15H2MFA acél kiindulási diszlokációsűrűsége egy nagyságrenddel kisebb volt, mint az általuk vizsgálté. A reaktortartály anyagban a korábbiak szerint 25%-os károsodást elszenvedett próbatestnél mértük a legnagyobb diszlokációsűrűséget (6,1 × 1014 / m2) ami Meyer és munkatársai által vizsgált anyag kezdeti értékének felel meg [Mayer et al., 2012]. A 15H2MFA anyagnál a diszlokációsűrűség csökkenés és a cellaméret növekedés ezután következett. A diszlokációsűrűség csökkenése vélhetően két egyidejű folyamat eredménye: mozgásuk közben bizonyos diszlokációk kioltják egymást és a diszlokációk a cellafalakba ütközve nem mozognak tovább. Ezek eredményeként a mikro-deformációs folyamatok a szemcsehatárokon zajlanak ezt követően, ahol a mikrorepedések keletkeznek.

A fárasztott minták diszlokációsűrűségét kétféle módon határoztuk meg; a TEM felvételekből a Keh-Weismann módszerrel és röntgen vonalprofil analízissel a 3.3 fejezetben leírtak szerint.
4. táblázat. A megszakított fárasztóvizsgálatok mintáin végzett röntgen-vonalprofil analízis eredményei. ρd a diszlokációsűrűség, M* a diszlokációk dipól jellegét adja, qd a diszlokációk él/csavar jellegét adja meg (térben középpontos szabályos rácsú acélra qd (él/csavar) = 1.3/2.7), <x>area a felülettel súlyozott szemcseméret (koherens szórótartomány).
| Minta | qd [-] | ρ [1014 m-2] | M [-] | <x>area [nm] |
|---|---|---|---|---|
| 15H2MFA kiindulási | 1,8±0.2 | 2,7±0.2 | 2,8±0.5 | 95±10 |
| 15H2MFA 5% | 1,8±0.2 | 3,9±0.3 | 2,2±0.5 | 103±10 |
| 15H2MFA 25% | 1,8±0.2 | 6,1±0.6 | 2,2±0.5 | 101±10 |
| 15H2MFA 50% | 1,8±0.2 | 3,7±0.3 | 2,2±0.5 | 106±10 |
| 15H2MFA 70% | 1,8±0.2 | 2,2±0.2 | 2,2±0.5 | 110±10 |
A 15H2MFA anyag vizsgálata során a TEM felvételekből a diszlokációsűrűség átlagértékét határoztuk meg. Az XRD mérésekből és a TEM felvételekből meghatározott diszlokációsűrűség értékek összehasonlítása látható a károsodási tényező függvényében a 10. ábrán.
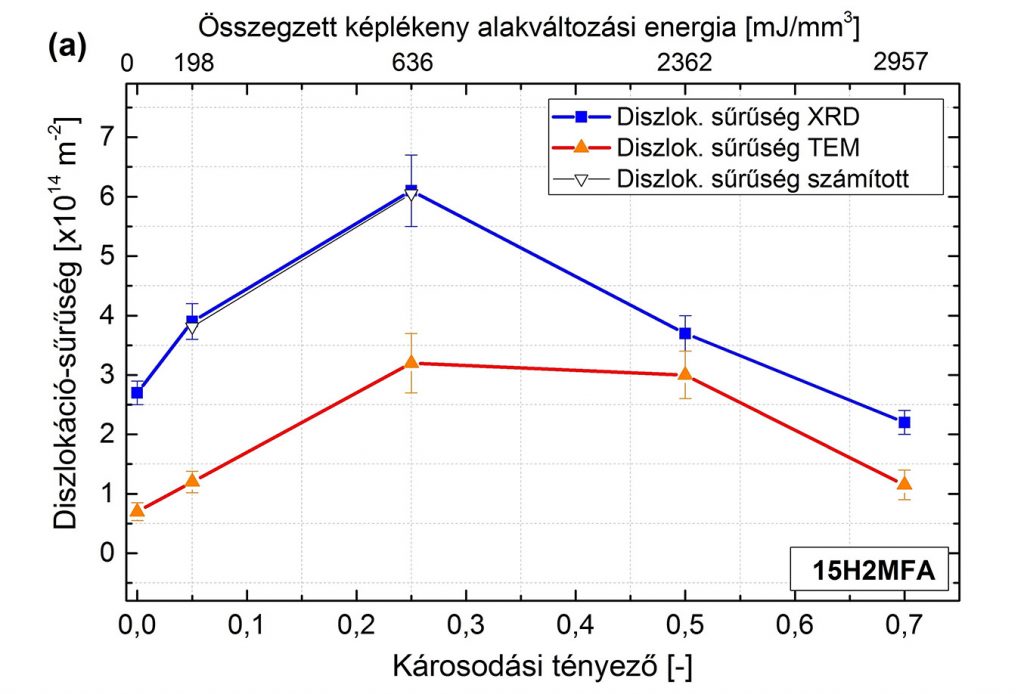
Az ábrából látható, hogy a kétféle módszerrel meghatározott értékek trendje azonos, mellyel az XRD mérések eredményeinek érvényességét igazoltuk [Mayer et al., 2012]. Az abszolút értékbeli különbségek a kétféle módszer (lokális és nem lokális) eltérő jellegéből adódnak. Az ábrából egyértelműen következik, hogy a fáradási folyamat során a vizsgált szerkezeti anyagoknak a diszlokációsűrűség változása nem monoton függvény szerint történik. Ez azt jelenti, hogy ha rendelkezésünkre áll egy ismeretlen károsodást elszenvedett minta, akkor a diszlokációsűrűségének mérésével az élettartam kimerültségének foka nem állapítható meg, mivel adott diszlokációsűrűséget két egymástól távol eső kifáradási állapotban is mérhetünk. A TEM vizsgálatokkal kiegészítve azonban a fentiek figyelembe vételével jó közelítéssel becsülhető a fáradás mértéke.
5.3 A KÁROSODÁS KINETIKÁJA ÉS MIKROSZERKEZETI HÁTTERE
A fáradás során lezajló mikroszerkezeti változások, és a mechanikai viselkedés anyagtudományi hátterének vizsgálata érdekében a megszakított fárasztóvizsgálatok mintáin végzett TEM és az XRD mérések eredményeit együtt elemezzük. A kísérleti anyag termomechanikus fárasztóvizsgálata során folyamatos ciklikus lágyulást mutatott, amely a mérések kezdeti szakaszán intenzívebb volt (UF = 0,05 eléréséig), majd a stabil ciklusok alatt a lágyulás mértéke jelentősen lecsökkent. A lágyulás szakaszán a 4. táblázat szerint a diszlokációsűrűség növekedését tapasztaltuk, amely formális ellentmondásban van a klasszikus képlékenységtani ismeretekkel. A folyamat megértésére a diszlokációk szabad úthosszának (l) elemzése ad lehetőséget az alábbiak szerint.
A diszlokációmozgás szempontjából közelítve a problémát, a képlékeny alakváltozási sebesség (![]() ) a diszlokációk Burgers vektorától (b), a diszlokáció mozgás átlagsebességétől (
) a diszlokációk Burgers vektorától (b), a diszlokáció mozgás átlagsebességétől (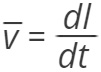 ), és a mozgó diszlokációk sűrűségétől (ρd) függ a következő képlet szerint [Cottrell, 1949]:
), és a mozgó diszlokációk sűrűségétől (ρd) függ a következő képlet szerint [Cottrell, 1949]:
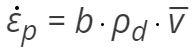 (1)
(1)
Mivel a b állandó és ρd nem változhat a diszlokációk mozgása nélkül, ezért az alakítási szilárdság egyértelműen a diszlokációk sebességéhez (![]() ) köthető [Gilman, 1961].
) köthető [Gilman, 1961].
A feszültség és a diszlokációsebesség között az alábbi empirikus összefüggés áll fenn [Partin et al., 2010]:
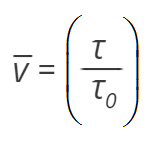 (2)
(2)
ahol τ a csúsztatófeszültség és τ0 állandó a v = 1 cm/s diszlokációsebességet okozó feszültséget reprezentálja [Prekel et al., 1968]. Az m anyagi paraméter a diszlokáció sebesség-feszültség együttható.
A fenti egyenletekből:
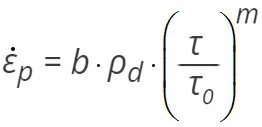 (3)
(3)
melyet átrendezve az alábbi formulát kapjuk:
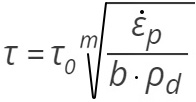 (4)
(4)
A (4) egyenletet két különböző fáradási állapotra felírva, és egymással osztva az alábbi összefüggés adódik:0
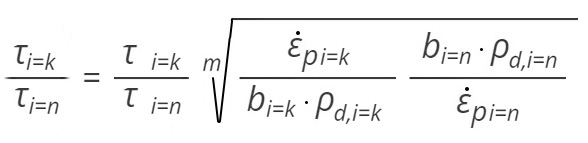 (5)
(5)
ahol az i index különböző (n és k ciklusszámokhoz tartozó) károsodással terhelt állapotokat jelöl.
Az alábbi mennyiségek nem változnak a ciklikus képlékeny alakváltozás során, ezért írható:
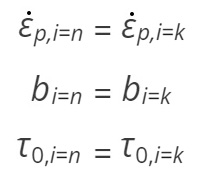 (6)
(6)
így (5) a következő formulára hozható:
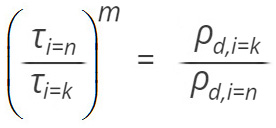 (7)
(7)
A különböző állapotokban a fárasztóvizsgálatok során elért alakítási szilárdságok arányának ismeretében, a (7) modellel a ciklusok során megvalósuló képlékeny alakváltozáshoz szükséges diszlokációsűrűség hányadost határozhatjuk meg. A diszlokáció sebesség-feszültség együttható értéke hasonló mikroszerkezetű nyomástartó edény acélokra m = 1 3 [Partin et al., 2010].
A diszlokáció sebesség hányadosokat a fenti képlet szerint kiszámítottuk a UF = 0-0,05 és a UF = 0,05-0,25 állapotokra a fárasztóvizsgálatok során rögzített alakítási szilárdságok értékéből, melyek 1,47 és 1,56 értékre adódtak a következők szerint:
A kezdeti (UF = 0) és a UF = 0,05 fáradási állapotok közötti diszlokációsűrűség növekmény számítása
A maximális feszültségek átlagértékének aránya a fárasztókísérletek során rögzített adatokból, UF = 0 és UF = 0,05 állapotra:

A (7) egyenlet figyelembe vételével a diszlokációsűrűségek aránya a két állapotra:
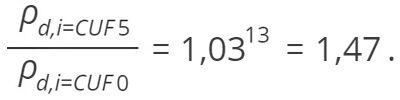
Az XRD eljárással meghatározott diszlokációsűrűség értékek a vizsgált állapotokban:
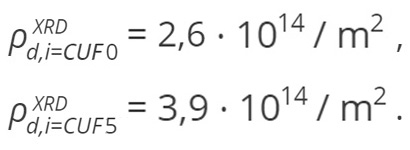
A (7) modellel számított diszlokációsűrűség értéke a UF = 0,05 állapotban:
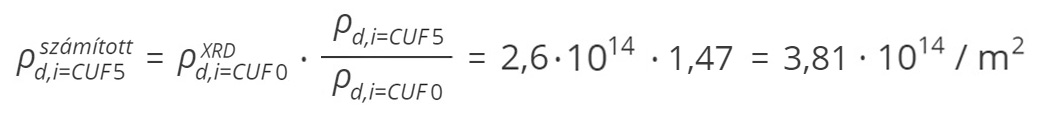
A UF = 0,05 és a UF = 0,25 fáradási állapotok közötti diszlokációsűrűség növekmény számítása
A maximális feszültségek átlagértékének aránya a fárasztókísérletek során rögzített adatokból UF = 0,05 és UF = 0,25 állapotra:
![]()
A (7) egyenlet figyelembe vételével a diszlokációsűrűségek aránya a két állapotra:
![]()
Az XRD eljárással meghatározott diszlokációsűrűség értékek a vizsgált állapotokban:
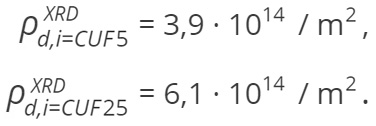
A (7) modellel számított diszlokációsűrűség értéke a UF = 0,05 állapotban:
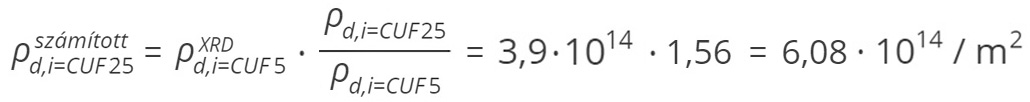 .
.
Az előző fáradási állapotra vonatkozó XRD eredmények felhasználásával a (16) modell segítségével kiszámíthatók az adott állapotra érvényes diszlokációsűrűségek. A diszlokációsűrűség a UF=0,05 állapotban , míg a UF=0,25-ra vonatkozóan értékre adódott. A modellből számított eredményeket a 4. táblázat ugyanarra az állapotra vonatkozó értékeivel összehasonlítva, azok igen jó egyezését állapíthatjuk meg, amelyből arra következtethetünk, hogy a ciklikus lágyulás során ezen az élettartam szakaszon mozgásra képes diszlokációk keletkeztek. A telítődési diszlokációsűrűség elérését követő tartományon (10. ábra) a modell láthatóan nem érvényes, amelynek oka a TEM felvételek (8. ábra) alapján, hogy a makroszkopikus képlékeny alakváltozás a mikroszerkezet szintjén különböző folyamatok mentén folytatódik, melyek a diszlokációk mozgása, a cellafalak deformációja és vándorlása. További ciklikus terhelés hatására a folyamat egyre inkább a klasszikus lágyulási mechanizmusok szerint zajlik, melyben a cellahatárok dominánsak, és a diszlokációsűrűség csökkenése, valamint a szubszemcse méret növekedése jellemzi [Mayer et al., 2012].
A fentiekből látható, hogy a fáradási élettartam első szakaszát (UF=0,05-ig) a diszlokációk cellákon keresztül történő szabad mozgása, és a kiválások Frank-Read forrásként működő diszlokáció-sokszorozó hatása uralja. A diszlokációk szabad úthosszát a cellaméret és a kiválások távolsága határozza meg. A fáradási folyamat előrehaladásával (UF=0,25) a diszlokációsűrűség eléri a maximum értékét a szabad úthosszak lecsökkenek, és a lágyulási folyamat kvázi-stabil módon folytatódik. További ciklikus terhelés hatására létrejövő diszlokációsűrűség csökkenés a források blokkolódásának, a diszlokációk kioltásának és a mozgó cellafalakba történő beépülésének következménye.
A mikroszerkezetben a legjobban érzékelhető változás az élettartam felétől tapasztalható, amelyet követően a dinamikus folyamatok megjelenése jellemez. Erre a cellahatárok elhajlása utal (8. (b) ábra). UF=0,70 elérése után a cellahatárok elveszítik irányítottságukat és vonaluk a TEM- képeken (9. ábra) helyenként megtörik, ami a korábbi állapotokban nem figyelhető meg. A karbid kiválások mérete is valamelyest megnő és rendszerint a cellahatárokon találhatók. Mindezek a jelenségek arra utalnak, hogy a ciklikus terhelés folyamán diffúziós folyamatok mennek végbe, amelyek következtében megindul a cellahatárok elmozdulása. Emellett a diszlokációsűrűség is csökken, egyre több cella belseje tűnik diszlokáció-mentesnek. Mindezek a (dinamikus) folyamatok elvezethetnek oda, hogy a kisszögű cellahatárok szerkezete átalakul, azok mozgásképessé válnak. Ezáltal a kialakult csúszási rendszerek elzáródhatnak, a csúszás/elmozdulás a diszlokációs mechanizmusról áttevődhet a szemcse- és cellahatárokba. Mivel utóbbiak már nem fekszenek benn valamilyen csúszási síkban, a határok menti elmozdulások, repedések kinyílásához vezetnek. Ezt a folyamatot erősíti a karbid kiválások jelenléte a határokban. A ciklusszám további növelésével a meghatározó repedés növekedésnek indul.
ÖSSZEFOGLALÁS
A kutatómunka során a próbatestek névleges kisciklusú fáradási élettartamáig végzett kísérletek eredményeire támaszkodva, az élettartam kiválasztott pontjáig megszakított fárasztóvizsgálatokat végeztünk. Az így öregített próbatestek transzmissziós elektronmikroszkópos (TEM) és röntgen diffrakciós (XRD) vizsgálatával nyomon követtük a fáradási alapstruktúra fejlődését és megvizsgáltuk a szerkezeti anyagok ciklikus mechanikai viselkedésének mikroszerkezeti hátterét. A kísérleti anyag ciklikusan lágyuló mechanikai viselkedést mutatott a fárasztás kezdeti szakaszán, ugyanakkor diszlokációsűrűsége növekedett az XRD mérések és a TEM vizsgálatok eredményei szerint. A hagyományos képlékenységi elméletek szerinti formális ellentmondás egy lehetséges feloldását a mozgásra képes diszlokációk vizsgálatával adtuk meg.
IRODALOMJEGYZÉK
Bereczki, P., Szombathelyi V., Krallics, Gy., 2014. Determination of flow curve at large cyclic plastic strain by multiaxial forging on MaxStrain System, International Journal of Mechanical Sciences, Vol. 84, p. 182.
Cottrell, H., 1949. Progress in Metal Physics, Theory of Dislocations. Vol. 1
Davies, L. M., 1999. A comparison of Western and Eastern nuclear reactor pressure vessel steels, International Journal of Pressure Vessels and Piping, Vol. 76, pp. 163–208.
Gilman, J. J., 1961. Dislocation motions and the yield strength of solids. ASTM International, Vol 283, p. 67.
Ginsztler, J., 1988. Thermal strain ageing and crack initiation during low cycle thermal shock fatigue. Theoretical and Applied Fracture Mechanics. Vol. 9. pp. 165-169.
Gorynin, I. V., 1998. Stuctural Materials for NPP Reactor Pressure Vessels in Russia, Fifth Intenational Conference on „Material Issues in Design, Manufacturing and Operation of NPP Equipment, Szentpétervár
He, P., Klimenkov, M., Möslang, A., 2014. Lindau, R., Seifert, H. J. Correlation of microstructure and low cycle fatigue properties for 13.5Cr1.1W0.3Ti ODS steel. Journal of Nuclear Materials, Vol. 455. pp. 167–173.
Lee, K. O., Hong, S. G., Lee, S. B., 2008. A new energy-based fatigue damage parameter in life prediction of high-temperature structural materials, Materials Science and Engineering A, Vol. 496, p. 471–477
Lee, Y. L., Pan, J., Hathaway, R., Barkey, M., 2005. Fatigue Testing and Analysis – Theory and Practice. Elsevier Butterworth–Heinemann. USA, MA
Lukács, J. 2012. Szemelvények a mérnöki szerkezetek integritása témaköréből. Miskolci Egyetem
Mayer, T., Balogh, L., Solenthaler, C., Gubler, E. M., Holdsworth, S. R., 2012. Dislocation density and sub-grain size evolution of 2CrMoNiWV during low cycle fatigue at elevated temperatures, Acta Materialia, Vol. 60 p. 2485–2496
Partin, K., Findley, K. O., Van Tyne, C. J., 2010. Microstructural and alloy influence on the low-temperature strengthening behavior of commercial steels used as plates. Materials Science and Engineering A Vol. 527 p. 5143
Prekel, H. L., Lawley, A., Conrad, H., 1968. Dislocation Velocity Measurements in High Purity Molybdenum, Acta Metallurgica, Vol 16.
Saji, G., Timofeev, K. 2009. Scientific paradigms of structural safety of aged plants—Lessons learned from Russian activities. Nuclear Engineering and Design, Vol. 239, p. 1614.
Shankar, V., Bauer, V., Sandhya R., Mathew M. D., Christ, H. J., 2012. Low cycle fatigue and thermo-mechanical fatigue behavior of modified 9Cr–1Mo ferritic steel at elevated temperatures. Journal of Nuclear Materials, Vol. 420. pp. 23–30.