A mikro képlékeny tartományból az általános folyásba való átmenet folytonosan vagy nem folytonosan egyaránt végbemehet. Az utóbbi esetben a feszültség–nyúlás diagramon a Hooke-féle egyeneshez csatlakozóan többé-kevésbé jelentős bizonytalanság lép fel (felső folyási határ). Az ezzel együtt járó εL nyúlást Lüders nyúlásnak nevezzük. Eközben egy majdnem homogén alakított tartomány jön létre (Lüders sáv), és a képlékeny alakváltozás a nem alakított tartományba hatol be (ez az eltérő fényvisszaverődés miatt folyási alakzatként válik láthatóvá). Az inhomogén alakváltozás a hideghengerléssel végzett lemezalakításkor vagy mélyhúzáskor nem kívánt jelenségnek tekinthető, amely megnövekedett felületi érdességhez vezet. Mivel a folyási vonalak ismét eltűnnek, amikor is a Lüders sávok a teljes tartományra már kiterjedtek, a lemezalakításkor arra kell törekedni, hogy az alakítás mértéke a Lüders nyúlás mértékét meghaladja. A Lüders sávok kiszélesedésének befejezése után az alakváltozás makroszkóposan nézve homogén lesz, és az alakítási szilárdság ismét növekedni kezd.
A felső folyáshatár megjelenését alapvetően az alakváltozást okozó diszlokációk és az idegen atomok közötti rugalmas kölcsönhatásra vezethető vissza. Cottrell feltevése szerint ebben a folyamatban főleg az éldiszlokációk és az intersztíciósan oldott atomok szerepe a meghatározó, amelyek a diszlokációk tágult tartományában helyezkednek el. Így az intersztíciós atomok Cottrell felhőket alkotnak, amelyek mozgása a rács torzulási energiájának csökkenése miatt gátolt. Csak a külső feszültség megnövekedése révén szabadulhatnak meg a diszlokációk az intersztíciós atomok alkotta felhőktől. Eközben a diszlokációk megsokszorozódnak, ami azt jelenti, hogy számos mozgásra képes diszlokáció képződik, mégpedig olyanok, amelyeknek a szabad úthossza viszonylag nagy. A képlékeny alakváltozás sebességét 
egy húzással igénybevett szerkezeti anyagban a következő egyenlet fejezi ki:
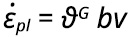
ahol ϑG – a mozgásra képes diszlokációk száma, b – a Burgers vektor, v – a diszlokációk átlagos mozgási sebessége. A diszlokációk átlagos sebessége az anyagra ható húzófeszültség nagyságával arányos, és egy állandó adott alakváltozási sebesség esetén a θG diszlokáció-sűrűség növekedésekor a v diszlokáció sebesség csökkenéséhez vezet, ami egy hirtelen feszültség-esésben mutatkozik meg. Kis alakváltozások esetén
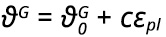
ahol 
– az alakítatlan állapotú anyagban jelenlévő mozgásra képes diszlokációk száma, c – állandó.
Ugrásszerű feszültségesés mindig akkor lép fel, ha kicsi, ami például színvas esetében a diszlokációknak az intersztíciósan oldott karbon és nitrogénatomok alkotta Cottrell felhők általi blokkolása miatt állhat elő.
Teljes cikk: Miért és milyen mértékben változhat a folyási nyúlás közben a feszültség?