1. Előzmények
Kutatói pályafutásom kezdetén, vagyis az 1960-as évek végén, a Vasipari Kutató Intézetben első feladatom egy Carl Zeiss Jena gyártmányú elektronoptikai berendezés üzembe helyezése és üzemeltetése, illetve a megrendelt és saját kezdeményezésű vizsgálatok végrehajtása volt. A berendezés az építőszekrény elvén épült fel, sajnálatos módon azonban csak két fokozata került piacra: egy hagyományos, 65kV gyorsító-feszültségű elektronmikroszkóp, és egy, az akkori időkben újdonságnak számító emissziós elektronmikroszkóp. Mivel ez utóbbi vizsgálati lehetőségei illeszkedtek legjobban a fénymikroszkópos technikához, kezdettől fogva ennek a berendezésnek a működtetésére fordítottam a figyelmemet.
Az emissziós mikroszkópban vezető anyagú tömbi minták felületének leképzésére volt lehetőség a fénymikroszkóp felbontóképességével közel megegyező vagy annál kissé jobb felbontással. A mikroszkópban polírozott vagy maratott, esetleg kissé tagolt felületű minták voltak vizsgálhatók. Az emissziós mikroszkópban a leképzéshez szükséges elektronokat háromféle gerjesztéssel lehetett a próbatestből kiváltani. A szoba- vagy annál kissé magasabb hőmérsékletű leképzést a próbatest felületének ionokkal vagy elektronokkal való bombázása tette lehetővé. A harmadik lehetőséget a termikus gerjesztés jelentette, amikor is a mintát egy viszonylag nagy teljesítményű elektronágyú segítségével olyan hőmérsékletre lehetett hevíteni, amelyen már a 20-30kV nagyságú gyorsító feszültség hatására a leképzéshez elegendő nagyságú elektronáram adódott. A berendezés működési elve a ’60-as, ’70-es évek szakirodalmában megtalálható, kiegészítésként itt csak azt említem meg, hogy a ’70-es évek végén egy nyugat-európai cég olyan emissziós elektronmikroszkópot fejlesztett ki, amelyben a mintából ultraibolya fény gerjesztette a minta elektron-kibocsátását.
1.1. Egy tanulságos baleset
Az első ismertetendő, és a hőtágulással kapcsolatos eset egy „balesethez” kapcsolódik. Az emissziós mikroszkópba a próbatestet – amelynek átmérője 9 mm, vastagsága 1 mm volt – egy próbatartó rúd segítségével lehetett bejuttatni. Maga a minta ennek a rúdnak a végén, egy speciális mintatartóban helyezkedett el, amely két lemezrugó segítségével kapta meg a gyorsító feszültséget. A mintatartó egy 50 mm hosszú, 10 mm átmérőjű kerámiarúdba illeszkedett. Ez a kerámiaszigetelő izolálta el a próbatartó rúd fémből készült, és a tömítést is biztosító részét a nagyfeszültségtől. Ezt a próbatartó rudat egy speciális mechanizmus segítségével lehetett a nagyvákuum alatt lévő mikroszkóp térben x és y irányban eltolni, a próbatartó tengelye körül forgatni, és a hevítést végző elektronágyú és az ún. „harang” alsó részét lezáró blende közötti magasságot változtatni. A próbatartó rúd mozgatását biztosító mechanika egy, az emissziós elektronmikroszkóp viszonylag nagy átmérőjű felső részéből is kiállt.
Az elektronmikroszkópos felvételek készítésekor a laboratóriumban csak egy vörös fényű világítótest volt bekapcsolva, ami a tájékozódást megnehezítette. Valamely váratlan esemény megtörténtekor előfordulhatott, hogy a mikroszkóp kezelője hirtelen, kellő körültekintés nélkül felállt, és a feje fölé benyúló próbatartó mechanikájába, illetve magába a próbatartó rúd végébe belefejelt. Egy ilyen alkalommal a próbatartó rúdba szorosan illeszkedő kerámiatest eltört, és szükségessé vált annak cseréje.
A berendezés gépkönyve igen részletes leírást tartalmazott minden egyes tisztítási, javítási és karbantartási műveletre, de ennek a kerámiatestnek a cseréjére nem találtam semmiféle utalást. Így hát saját kútfőm szerint igyekeztem a beletörött szigetelődarabot először eltávolítani, majd a tartalék alkatrészek között megtalálható új kerámiatestet a próbatartó rúd zsákfuratába beilleszteni.
A fémek és keramikus anyagok hőtágulásával kapcsolatos eset valójában itt kezdődik. Kézenfekvőnek látszott, hogy először a beletörött kerámiadarabot kellett eltávolítani. A rozsdamentes acélból készült próbatartó rúdnak azt a végét, amelyben a beletörött kerámiadarabka található volt, egy hegesztőpisztoly „lágy” lángjával felmelegítettem, így ez a kerámiadarabka szinte kiesett a zsákfuratból.
A probléma akkor kezdődött, amikor a tartalék alkatrészek között található új kerámia szigetelőt megpróbáltam a próbatartó rúd előmelegített végébe beletolni. Ez csak néhány milliméternyi mélységig sikerült, mert a próbatartó rúd végében lévő zsákfurat fala „ráfogott” a kerámiatestre, annak ellenére, hogy a kerámiák rossz hővezetők. Mivel a vizsgálandó minta pozíciója a mikroszkópban pontosan meghatározott volt, a nem megfelelő mélységig betolt kerámiatesttel a próbatartó rúd nem tölthette be feladatát.
Ezen a ponton a „Mitől foltos az acéllemez” című esettanulmányban már említett módszert is alkalmazhatnám, vagyis azt, hogy a jelenséget először analizáljuk, majd az analízis eredményéből létrehozzuk a szintézist, majd ennek alapján javaslatot teszünk a megoldásra. Ebben az egyszerű esetben ez talán túlzás, így hát mindjárt a megoldást mutatom be.
Kétszer-háromszor megismételve a sikertelen kísérletet, új utat kellett választanom. Ahhoz, hogy a próbatartó rúd zsákfuratának fala ne fogjon rá a kerámiatestre, el kellett kerülni annak gyors lehűlését. Ennek legegyszerűbb útja az volt, hogy magát a kerámia testet is előmelegítettem a próbatartó rúd végének előmelegítési hőmérsékletére. Az előmelegített kerámiatest minden nehézség nélkül betolható volt a zsákfuratba a szükséges, kb. 10 mm mélységig.
Mivel ez a „baleset” még a berendezés garanciális ideje alatt történt, javasoltam a gyártó cég képviselőjének, hogy a kerámiatest cseréjére vonatkozó utasítást vegyék be a gépkönyvbe. Az általam javasolt megoldást a cég képviselői értékelték, de a gépkönyv módosítására – annak költséges módja miatt – nem volt mód, de megígérték, hogy minden egyes új berendezés átadásakor felhívják erre az esetre az aktuális üzemeltető figyelmét.
1.2. Hőmérsékletmérés a minta hőtágulása alapján az emissziós elektronmikroszkópban
Vizsgálataim során a legérdekesebb jelenségeket a nagy hőmérsékleten végzett vizsgálatok közben figyelhettem meg, ezért az időm nagy részében a termikus emissziós képalkotást alkalmaztam. Ennél a leképzési módnál ugyanis az egyes krisztallitok eltérő árnyalatban jelennek meg, mert a kontrasztot meghatározó kilépési munka függ a kristálytani orientációtól, ezért az újrakristályosodási és átalakulási folyamatok közvetlenül és késleltetés nélkül, azonnal láthatóvá válnak. Figyelmem elsősorban az átalakuló acélok ausztenitjének szemcsedurvulási folyamataira irányult [1]. Ez a munka szerves folytatása volt a leobeni Montanuniversitäten Roland Mitsche professzornál végzett nagyhőmérsékletű fénymikroszkópos munkáimnak. A nagyhőmérsékletű fény- és emissziós elektronmikroszkópos képalkotás jellegzetességeit az 1. ábra képfelvételével szemléltetem.

(a) Vacuthermen készült felvétel, (b) ER-Z6 emissziós elektronmikroszkóppal készült felvétel.
A nagyhőmérsékletű emissziós elektronmikroszkópos vizsgálatok egyik kritikus pontja a próbatest hőmérsékletének pontos mérése és szabályozása volt. Az eredeti megoldás egy meglehetősen nehézkesen alkalmazható összehasonlító pirométeres mérési módszer volt, amely tapasztalatom szerint csak nagy hibával terhelt hőmérsékleti adatokat szolgáltatott. Két megfigyelés vezetett az eisenhüttenstadti Stahlkombinat által a későbbiekben megvett know-how kidolgozásához [2].
Az első megfigyelés arra vonatkozott, hogy ha a képalkotáshoz az elektronokkal való gerjesztést választottam, a legritkább esetben sikerült éles felvételt készítenem. A megfelelő mélységi élességű felvételhez ugyanis a legkisebb kontrasztblendét kellett választanom, ehhez viszont hosszú expozíciós idő tartozott. Az üveglemezek előhívásakor sok esetben azt tapasztaltam, hogy a képen látható jellegzetes területek egy határozott irányba eltolódtak. Ezzel a problémával az ionokkal való gerjesztéskor nem találkoztam, és így arra a következtetésre jutottam, hogy a szekunder elektronokkal való leképzéskor a minta a gerjesztés hatására felmelegszik, és a felvételen tapasztalható „elmászás” magának a mintának, illetve a mintatartó hőtágulásának a következménye.
Ez a jelenség még szembetűnőbb volt, amikor termikus emissziós üzemmódban dolgoztam. Mivel elsősorban szemcsenövekedési és durvulási folyamatokat kívántam követni, nagyon lényeges volt, hogy a képernyőn a mintának mindig ugyanaz a része jelenjen meg. Ezt úgy igyekeztem elérni, hogy a vizsgálat kezdetekor a képernyő közepére vittem a minta egy jellegzetes elemét, például egy zárványt vagy egyéb részecskének a képét, és ezt a kiválasztott pontot a próbatartó rúd mozgatására szolgáló mechanizmussal mindig visszavittem a képernyő közepére, kompenzálandó a hőtágulást. Annak ellenére, hogy a mintát hevítő elektronágyú teljesítményét nem változtattam, azt tapasztaltam, hogy a kiválasztott pont az idő előrehaladtával mindig „elmászik” a képernyő közepétől, tehát a próbatartó rúd helyzetét állandóan kontrollálnom kellett.
Ezek a megfigyelések vezettek a korábban már említett know-how kidolgozására, nevezetesen a nagyfeszültségen lévő minta hőmérsékletének annak hőtágulásán alapuló méréséhez. Magát a hőmérséklet-mérő rendszert Dilatherm-nek neveztem el, amelynek műszaki rajzát a 2. ábra mutatja.
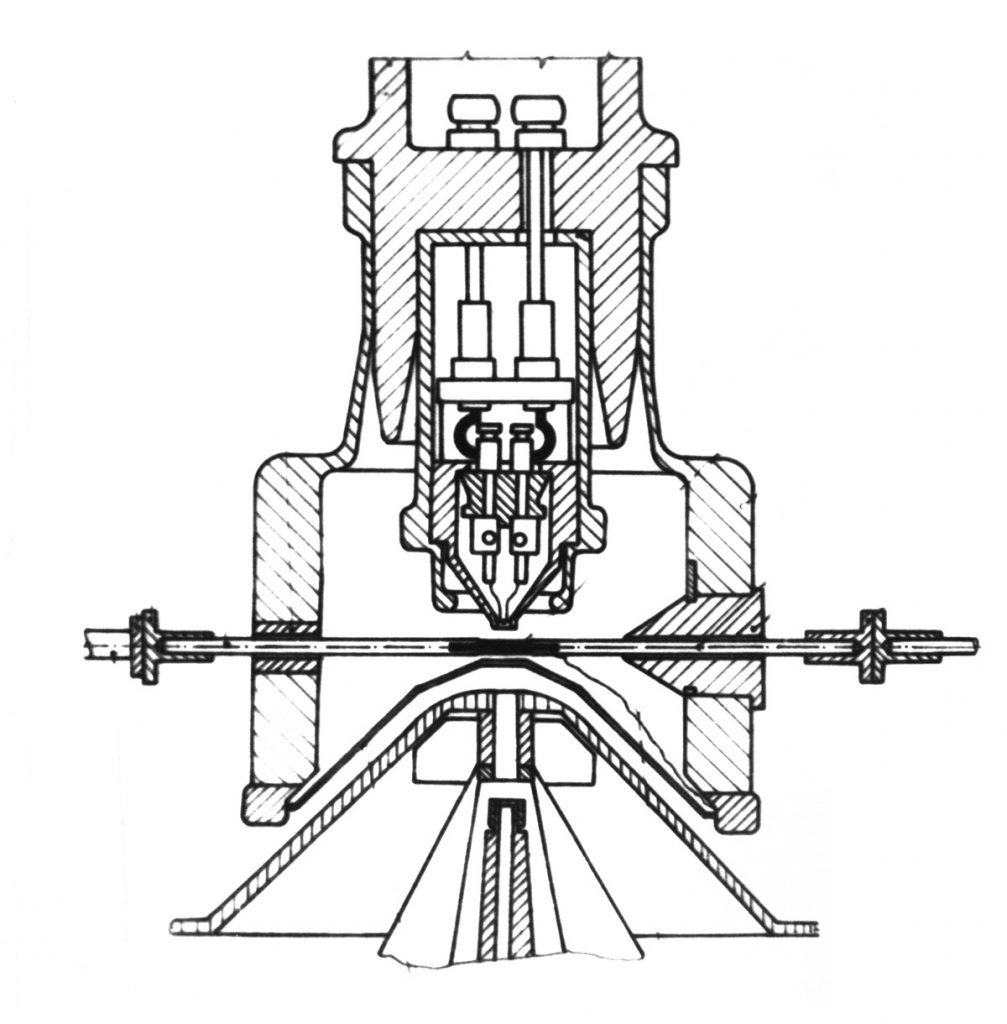
Ezt a megoldást egy, a ’70-es évek elején tartott berlini konferencián, az Arbeitstagung für Elektronenmikroskopie-n előadás formájában ismertettem, és lényegében a konferencia tudományos titkársága javasolta az eisenhüttenstadti acélművek kutatórészlegének, hogy vegye meg a kidolgozott módszer licencét.
A megoldás lényege az, hogy az emissziós elektronmikroszkóp fejébe egy dilatométert építettem be. Természetesen ehhez az eredeti mintatartót helyettesítenem kellett egy olyan szerkezettel, amely képes volt a kisméretű minta hőtágulását kivezetni. Ehhez kb. 2 mm átmérőjű kvarccsövecskéket használtam. A kvarccsövecske egyik vége egy vákuumtömören elhelyezett induktív útadóhoz csatlakozott, míg a másik vége az állandó hőmérsékleten lévő mikroszkópfej falához támaszkodott. Olyan megoldást alkalmaztam, amely még lehetővé tette a mikroszkópfej mechanikus centrálását is. Magát a mintát úgy alakítottam ki, hogy annak két szemben lévő oldalán egy-egy 3-4 mm hosszú, a kvarccsövecske furatába illeszkedő csapocska volt. A minta a nagyfeszültséget egy, az arra ponthegesztett platinaszálon kapta meg. Hitelesítéskor a gyorsító-feszültséget ki kellett kapcsolni, és a mintára hegesztett platina-platinaródium termoelem segítségével mértem a hőmérsékletet. A hitelesítő görbét egy x-y íróval vettem fel, és vizsgálat közben az adott hőtáguláshoz tartozó hőmérsékletet fogadtam el a minta hőmérsékletének. Ez a megoldás természetesen csak akkor volt megfelelő pontosságú, ha a mintában nem játszódtak le fajtérfogat-változással járó folyamatok. Ez a megállapítás az átalakuló acélok ausztenites állapotban lejátszódó folyamataira nézve igaznak bizonyult. A 3. ábrán egy átalakuló acél ausztenitjében lezajló ikerképződés figyelhető meg.

2. A hőtágulás jelenségének egyszerű modellje
Ezek az emissziós elektronmikroszkóppal kapcsolatos megfigyelések talán kellően megvilágítják a hőtágulás jelentőségét, és az első tárgyalt eset arra is alkalmasnak látszik, hogy ezt a jelenséget az anyagtudományi ismeretek mai szintjén részletesebben megvilágítsuk, választ keresve például arra, hogy a fémes anyagoknak miért nagyobb a fajlagos hőtágulása, mint a keramikus anyagoké.
Valamely fizikai jelenség, esetünkben a hőtágulás jelenségének értelmezésekor általában valamilyen modellből indulunk ki. A választott modelltől elvárjuk, hogy a jelenséget bizonyos szintig helyesen írja le, és a modell alapján a legfontosabb kérdésekre egyértelmű választ adjon.
Ismert, hogy anyagaink 1 mólnyi mennyiségében az Avogadro-féle számnak megfelelő számú atom van. Ez a szám 6×1023-t jelent. Elvileg tehát valamely tömbi anyag hőtágulásának leírásakor igen nagyszámú atom együttes viselkedését kellene leírni, amely még mai adottságaink birtokában sem képzelhető el.
A hőtágulás jelenségének értelmezéséhez a lehető legegyszerűbb modellt választjuk. A modell alapján bizonyos kiinduló feltételek és ismeretek birtokában választ kell kapnunk arra a kérdésre, hogy anyagaink a hőmérséklet növekedése közben miért tágulnak.
Kísérleteinkből tudjuk, hogy 0 K-hez közeledve a térfogati és a lineáris hőtágulási együttható is 0-hoz tart, továbbá, állandó hőmérsékleten anyagaink térfogata nem változik, hacsak bennük nem játszódik le valamilyen fázisátalakulási folyamat. Ez utóbbi kísérleti eredmény egyben azt is jelenti, hogy állandó hőmérsékleten az atomok közötti távolság lényegében nem változik. A modell elemzésekor lényegében csak azt a mechanikából átvett ismeretet alkalmazzuk, miszerint egyensúlyi helyzetben az atomra ható erők eredője 0.
A választott, szinte a végtelenségig leegyszerűsített modell lényegében két atom kölcsönhatását tárgyalja, és ennek a kölcsönhatásnak a jellegéből vezeti le a kísérleti eredmények során tapasztaltak magyarázatát. A modell két egymás mellett lévő, azonos tulajdonságú és egymáshoz viszonyítva egyensúlyi helyzetben lévő atomból áll. A modell elemzésekor először a helyzetet statikusan, az atomok között ébredő taszító- és vonzóerők jellege alapján elemezzük, majd figyelembe vesszük azt a körülményt is, hogy 0 K-nél nagyobb hőmérsékleten az atomok tömegközéppontjuk körül rezgőmozgást végeznek.
2.1. A statikus modell
A helyzet tárgyalásához tekintsük meg a 4. ábrát. A függőleges tengely pozitív tartományában két atom között ébredő taszítóerőnek, míg a negatív tartományban a vonzóerőnek a két atom közötti távolság függvényében való változása látható. Tudjuk, hogy a taszítóerő a két atom közötti távolság függvényében erősebben változik, mint a vonzóerő. Matematikailag ez úgy fejezhető ki, hogy a taszítóerő változását leíró hiperbolikus függvény kitevője nagyobb, mint a vonzóerőt leíróé.
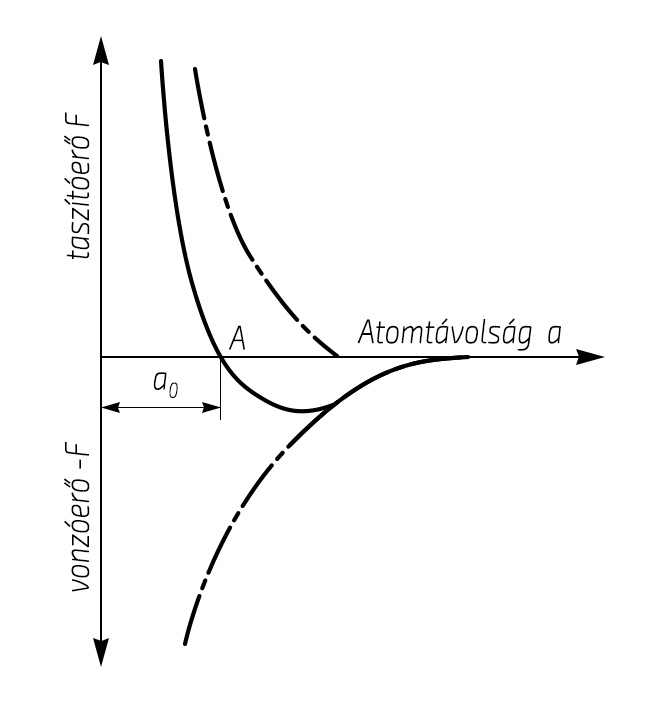
A taszító- és vonzóerő egymáshoz viszonyított értékét vizsgálva belátható, hogy az origóban lévő atom helyzetétől bizonyos a0 távolságban, vagyis az A pontban ez a két erő kiegyenlíti egymást, azaz ebben a pontban az a0 távolságra lévő atomra nem hat erő.
Az A pontban lévő atomra – azt az egyensúlyi helyzetből kimozdítva – a taszító- és vonzóerők különbsége által meghatározott eredő erő fog hatni. Ezt az eredő erőhatást jelző görbét a 4. ábrán szaggatott vonallal jelöltük. A taszító- és vonzóerők jellegéből következik, hogy az A pontban lévő atomra az origóban lévő másik atomhoz közeledve az erőteljesen növekvő taszítóerő, míg ellenkező irányú elmozduláskor a vonzóerő kerül túlsúlyba. Lényeges, hogy az eredő erő a két atom közötti távolság függvényében nem lineárisan változik. Ezt a jelzőt fogjuk megkülönböztető jelzőként használni a továbbiakban is.
2.2. A dinamikus modell
A statikus modellel az atomok egyensúlyi helyzetét értelmezni lehetett, de a hőtágulás jelenségére vonatkozóan ez a modell még nem szolgáltat információt.
A dinamikus modell tárgyalásakor abból az ismert tényből kell kiindulni, hogy az atomok tömegközéppontjuk körül (azaz a rácspontjuk körül) rezgő mozgást végeznek, amelynek frekvenciája 1012-1013 Hz, és a rezgés amplitúdója a hőmérséklet növekedésével növekszik.
A rezgést végző atom mindenkori helyzetét a rá ható erők átlagértéke szabja meg. A nagy rezgési frekvencia miatt az átlagolás időtartama akár nagyon rövid is lehet.
Ahogy azt már említettük, a statikus és a dinamikus modell együttes figyelembe vételével két tapasztalati és mérésekkel megerősített tényre kell választ kapnunk.
1. kérdés: Állandó hőmérsékleten miért nem lép fel a hőtágulás jelensége, vagyis miért nem változik meg ebben az esetben az atomok rezgésközéppontjának helyzete?
2. kérdés: A hőmérséklet növekedésével miért következik be a hőtágulás, vagyis miért növekszik a rezgést végző atomok rezgésközéppontjai közötti távolság?
Erre a két kérdésre akkor kaphatunk egyértelmű választ, ha az alábbi négy esetet elemezzük. Ezeket az eseteket rendre A, B, C és D betűkkel jelöljük:
- A. Az első feltételezett esetben az atomra ható erők eredője lineáris, és a rezgőmozgás szigorúan harmonikus.
- B. A második esetben az atomra ható erők eredője nem lineáris, de az atom rezgőmozgása szigorúan véve harmonikus.
- C. A harmadik esetben az atomra ható erők eredője lineáris, de az atom rezgőmozgása szigorúan véve nem harmonikus.
- D. A negyedik esetben az atomra ható erők eredője nem lineáris, és az atom rezgése szigorúan véve nem harmonikus.
Először az atom állandó hőmérsékleten lévő változatlan helyzetének követelményét vizsgálva megállapíthatjuk, hogy a B és C esetben az atomra ható erők eredőjének 0 értéke nem teljesülhet, ezért ezt a két esetet további elemzéskor eleve kizárhatjuk. Az atomra ható erők eredőjének 0 értéke az A esetben feltétel nélkül teljesül, míg a D esetben csak bizonyos feltételek mellett teljesülhet, vagyis akkor, ha a nem harmonikus rezgőmozgás amplitúdója úgy változik meg, hogy a taszító és vonzóerők kiegyenlítik egymást. Erre elvileg megvan a lehetőség.
A növekvő hőmérséklet hatására bekövetkező tágulást az A eset figyelembe vételével nem lehet értelmezni, hiszen a rezgési amplitúdó bármely mértékű növekedésekor az eredő erő mindenkor 0 marad, hiszen az erők eredője lineáris. A hőmérséklet növekedésével bekövetkező hőtágulás értelmezésekor az A esetet egyébként is kizárhatjuk, mert a statikus modellből következett, hogy a taszító- és vonzóerők eredője nem lineáris. Ezzel ellentétben a D esetben, amikor az amplitúdó növekszik, az egyensúlyi helyzetben kialakult erőegyensúly megbomlik, és az új, a növelt hőmérsékletnek megfelelő egyensúlyi helyzetben egy szigorúan véve nem harmonikus rezgőmozgás kialakulásával lehet számolni. Az elmondottak elemzéséhez az 5. ábra négy vázlata nyújt támpontot.
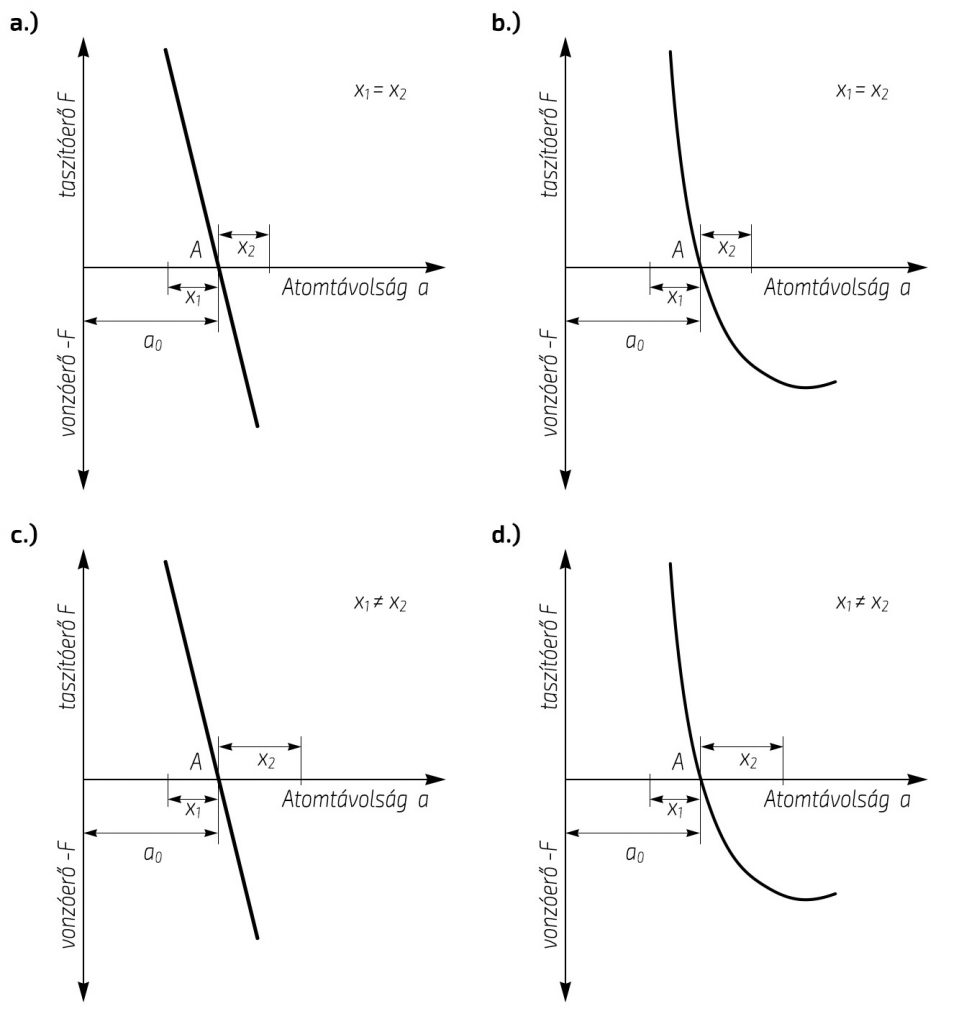
a) A eset: Lineáris eredő erő/harmonikus rezgés. b.) B eset: Nemlineáris eredő erő/harmonikus rezgés.
c.) C eset: Lineáris eredő erő/nem harmonikus rezgés. d.) D eset: Nemlineáris eredő erő/nem harmonikus rezgés.
Az elmondottak alapján látható, hogy mindkét felvetett kérdésre a végtelenül leegyszerűsített modell alapján is választ kaptunk. Hangsúlyozni kell azonban, hogy a válaszok csak olyan mélységig állják meg a helyüket, mint amilyen mértékben a választott modell helyes volt. Megjegyzem, hogy ennek az értelmezésnek az alapgondolata a [3] irodalomban megtalálható, de az ott ismertetett gondolatsor nem adott magyarázatot arra a kérdésre, hogy állandó hőmérsékleten miért nem játszódik le a hőtágulás folyamata. Ugyanakkor a sorok között az is kiolvasható, hogy [3] szerzői szintén arra a következtetésre jutottak, hogy a hőtágulás jelensége csak a D esetben tárgyalt feltételek érvényesülésekor következik be.
A modell alapján értelmezhető az a kísérleti tény is, hogy a 0 K-hez közelítve a tágulási együtthatók 0-hoz közelednek, hiszen mély hőmérsékleten a rezgési amplitúdó és az eredő görbe jellege is az előbb tárgyalt A esethez közelít. A keramikus anyagok hőtágulása pedig azért kicsi, mert a teljes vizsgált hőmérséklet-tartományban az A esetben tárgyalt helyzethez közeli állapot érvényesül, míg a fémek viselkedése sokkal inkább a D eset szerinti. Ez a különbség a fémes és a keramikus anyagokban ható kötőerők eltérő jellegére vezethető vissza.
Irodalom
[1] Verő Balázs: Az átalakuló acélok ausztenitjének sokkristályos állapota. Kandidátusi értekezés, Budapest, 1980.
[2] Dilatherm. Nemzetközi licencszerződés az eisenhüttenstadti acélművel.
[3] Schatt, Werner- Worch, Hartmut: Werkstoffwissenschaft, Deutcher Verlag für Grundstoffindustrie Stuttgart, 1996. 476. oldal.