Előzmények
Ahogy azt ennek a blognak a bevezetőjében írtam, szakmai múltamból olyan témákat szándékoztam feleleveníteni, amelyek még a VASKUT-as múltamhoz kötődnek. Valóban volt néhány ilyen eset is, de az esettanulmányok többsége későbbi pályafutásomhoz, akár napjainkban felvetődött témákhoz kapcsolódott.
Ez az esettanulmány azonban tényleg VASKUT-as időkhöz, mégpedig a ’70-es évek közepéhez, végéhez kötődik. Ugyanakkor – ahogy azt a Fekete Balázs által írt „Reaktortartályok kisciklusú fáradása” című tanulmány bevezetőjében is említettem – a ’70-es években megismert elmélet és az ennek alkalmazásával elért eredmények mintegy 40 év után váltak ismét aktuálissá.
Első kutatási témáim a hidegen hengerelt, lágyított acéllemezek folyási határának csökkentésére irányultak, és ennek kapcsán szükségszerűen fel kellett tárni az acélok folyási jelenségének mechanizmusát. Az elért eredményekről egy Salgótarjánban megtartott hidegalakító konferencián számoltam be, amelyen a kor gyakorlatának és lehetőségeinek megfelelően NDK-beli kollégák is részt vettek. Már az előadás elhangzása után is többen érdeklődtek, de az igazi meglepetés néhány héttel a konferencia után ért. Megjelent ugyanis előzetes bejelentkezés után a Német Demokratikus Köztársaság budapesti nagykövetségének tudományos attaséja és titkára, és személyesen engem keresve azt kérték, hogy adjam át nekik az előadásom kéziratát és diáit. Ezt meg is tettem. Az anyag további sorsáról visszajelzést nem kaptam. A Dunai Vasmű szakemberei – élükön dr. Horváth Ákossal – értékelték a munkánkat, és a folyási határ csökkentése és a folyási vonalak eltüntetése érdekében alkalmazott dresszírozó hengerlés optimális fogyási értékének megállapításakor a Vasipari Kutató Intézetben elért eredményekre támaszkodtak. Ebben az esettanulmányban azonban csak a címben megfogalmazott problémával foglalkozom, és a dresszírozás témakörét egy későbbi anyagban fogom tárgyalni.
E jelenségek értelmezésekor a korábbi esettanulmányokban már többször alkalmazott módszert követtem, vagyis az analízis – munkahipotézis – szintézis útvonalat kell követnünk a problémák megoldásához.
A lágyacélok folyási jelensége
A folyás a lágyacélok szakítóvizsgálat közbeni viselkedésének legszembetűnőbb jelensége. Közismert, hogy a lágyított állapotú lágyacélok szakítása közben a maradó alakváltozás a felső folyási határon kezdődik meg, majd egy jelentős feszültségcsökkenést követően közel állandó feszültségen alakul ki a folyási nyúlás, majd ezt az alakítási keményedés szakasza követi. A lágyacélok szakítódiagramjának kezdeti szakaszát szemlélteti az 1. ábra, külön kiemelve a folyási nyúlás szakaszát, ahol érzékeltettem, hogy a vizsgálati eredmények szerint a folyási nyúlás közben is feszültségváltozás tapasztalható.
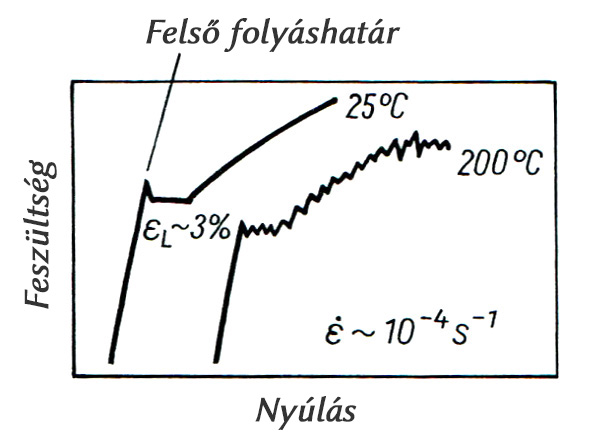
Az is közismert, hogy a felső folyási határon meginduló képlékeny alakváltozás az ún. Lüders-frontok kialakulásával jár együtt, és ezeknek a frontoknak a mozgásával alakul ki a folyási nyúlás. Ez a szakasz akkor fejeződik be, ha a szakító próbatest teljes térfogatában lezajlik a folyási nyúlás, és megkezdődik a keményedés szakasza.
A Lüders-frontok mozgását jól meg lehet figyelni polírozott felületű vagy vékony oxidhártyával fedett próbatestek szakítása közben. Ezt szemlélteti a 2. ábra felvétele [1]. Számos lágyított állapotú próbatest szakítása közben megfigyelhettem, hogy a folyási nyúlás közbeni terhelés- illetve feszültségváltozás mindig akkor következik be, ha a próbatestben egy új Lüders-tartomány alakul ki, vagy a mellette lévővel egyesül.
Ezeket a megfigyeléseket egy 1973-ban megjelent, A szakítódiagram kezdeti szakaszának fémtani, képlékenységtani elemzése lágyacélok esetén című dolgozatunkban [2] foglaltuk össze.
![2. ábra. Egy szakító próbatest felületén megfigyelhető Lüders-tartományok vázlatos rajzolata (a) illetve a rajzolatról készült felvétel (b) [1]](https://www.anyagtudomany.eu/wp-content/uploads/2021/11/luders-2ab-1024x337.jpg)
A folyási jelenség leírására még visszatérek, nevezetesen a [3] irodalom alapján. Az ott, a Streckgrenzeerscheinungen című fejezetben található leírás alkalmas arra, hogy megállapítsuk, hogy az általam végzett megfigyelések és elméleti megfontolások eredményei mely pontokon támasztják alá, illetve cáfolják az irodalmi adatokat.
A ’70-es évek technikai feltételei ennek a jelenségnek részletesebb kísérleti tanulmányozását nem tették lehetővé, de már akkor megszületett az a gondolat, hogy a feszültség-változást kapcsolatba lehet hozni a folyási nyúlást okozó, mozgásra képes diszlokációk számának megváltozásával.
A jelenség analízise
A következőkben azokat az elméleti eredményeket tárgyalom, amelyek a folyási jelenség fémtani értelmezéséhez szükségesek. Tárgyalom a képlékeny alakváltozás diszlokációs elméletének, a Cottrell-féle modellnek és a feszültség-relaxációs módszernek a lényegét.
A maradó alakváltozás diszlokációs elmélete
A ’60-as évek végére már szakmai körökben közismertté vált a képlékeny alakváltozás diszlokációs mechanizmusa. Jól emlékszem arra, hogy 1967-ben a Balatonszéplakon rendezett Kohászati Anyagvizsgáló Napokon édesapám, Verő József professzor plenáris előadásában először beszélt a kohászok szakmai közössége előtt a diszlokációkról, illetve az alakváltozás diszlokációs mechanizmusáról.
Kezdő kutatóként felfigyeltem a témakör újdonságértékére és jelentőségére, és igyekeztem ezen a területen elmélyíteni tudásomat. A Fémtani Osztályon lévő házi könyvtárban számos alapvető anyagtudományi könyv volt megtalálható, többek között Cotrell H.-nak a makroszkópos maradó alakváltozás és az alakváltozás diszlokációs mechanizmusa közötti kapcsolatáról szóló könyve.
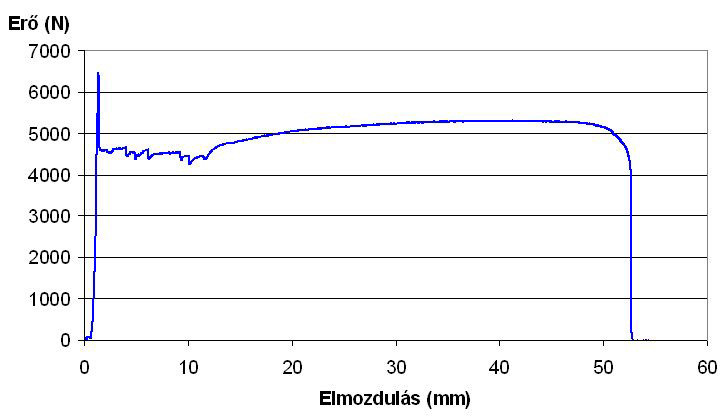
Természetesen, ennek a témakörnek az áttekintése nem lehet ennek az esettanulmánynak a feladata, így hát a maradó alakváltozás diszlokációs mechanizmusáról csak egyetlen ábrát hívok segítségül. A 3. ábrán a maradó alakváltozás folyamatának három egymást követő lépése tanulmányozható. Az 3.a ábrában a kristályrács egy kiválasztott részletében egy, a csúszósíkban mozgó diszlokáció vonala látható.
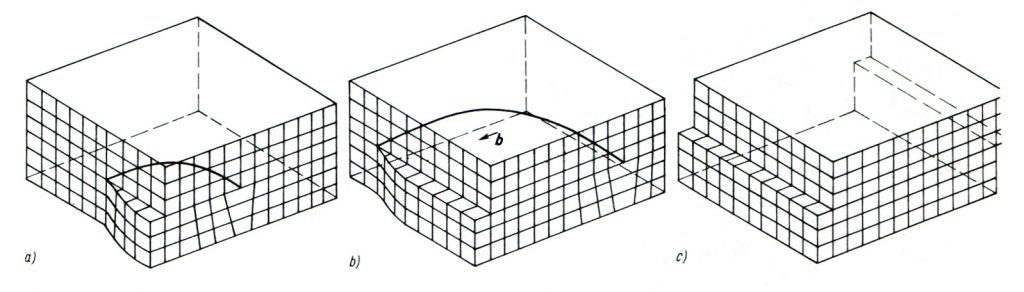
Ez a diszlokáció a kristályra ható τ* feszültség hatására balról jobb felé mozoghat. Gondosan megfigyelve ezt a helyzetet, megállapíthatjuk, hogy ez a diszlokáció-vonal a kristály részlet baloldali felületén tisztán csavar jellegű, míg annak elülső felületén tisztán él jellegű. Az is megállapítható, hogy a baloldali felület elülső élén megjelenő lépcső, vagyis a diszlokáció Burgers-vektora párhuzamos ezen a felületen a diszlokáció-vonallal, jelezve a korábbi megállapításunk helyességét, miszerint ezen a felületen a diszlokáció csavar jellegű. Ha a kristály elülső felületén a felületre kifutó diszlokáció-vonalat körbejárjuk, akkor könnyen megállapíthatjuk, hogy ezen a felületen a diszlokáció vonala és Burgers-vektora egymásra merőleges. Ebből az az alapvető megállapítás is leszűrhető, hogy egy adott diszlokáció-vonal mentén a Burgers-vektor irány- és nagyság szerint állandó marad, és a diszlokáció vonala bármely pontban felbontható egy él- és csavar komponensre.
Ebben a nagyon egyszerű modellben is szerepelnek már az alakváltozási sebességet meghatározó Cotrell-féle összefüggés tényezői, a mozgásra képes diszlokációk ρ sűrűsége, b Burgers-vektora és a diszlokáció-vonalra ható τ* tényleges feszültség.
A 3. ábrán szereplő tényezőkből már származtatott jellemzőket is definiálhatunk, és ha az ábrán bemutatott, egymást követő lépésekhez időtartamokat is rendelünk, akkor a Cottrell-féle elméletben alapvető szerepet játszó ![]() alakváltozási sebességhez is eljutunk .
alakváltozási sebességhez is eljutunk .
A kristályrészlet x irányú megnyúlása az adott esetben éppen b Burgers-vektornyi, hiszen az egyetlen diszlokáció vonalnak a kristályrészleten való áthaladása egy ilyen méretű lépcsőt hoz létre a kristályrészlet jobb oldalán. Ezt a megnyúlási értéket a kristály x irányú, és rácsparaméter egységekben kifejezett méretével osztva kapjuk meg az ε fajlagos nyúlást.
A 3. ábrán vázolt elemi alakváltozás folyamatának kezdő pillanatát az időben visszamenőleg ahhoz a pillanathoz viszonyítva jelöljük ki, amikor a diszlokáció vonal elérte a kristályrészlet baloldali, elülső élét. A folyamat előrehaladását bemutató a, b és c vázlatokhoz rendeljünk sorra Δt1, Δt2 és Δt3 időtartamokat. Ezeknek az adatoknak a birtokában már az ismert összefüggések alapján az ![]() alakváltozási sebességet és a v diszlokációsebességet egyértelműen definiálni tudjuk.
alakváltozási sebességet és a v diszlokációsebességet egyértelműen definiálni tudjuk.
A diszlokációsűrűséget kétféleképpen is meghatározhatjuk, vagy úgy, hogy a diszlokáció vonal hosszát osztjuk a kristályrészlet térfogatával, vagy pedig úgy, hogy megszámláljuk a kristályrészlet elülső felületére kifutó diszlokáció vonalak számát, és osztjuk ennek a felületnek a területével.
A diszlokációk mozgását meghatározó τ* tényleges feszültség értelmezésével majd a Cottrell-elmélet ismertetése után foglalkozom, de már itt megemlítem, hogy ez a csúsztatófeszültség nem azonos a csúszósíkban ható csúsztatófeszültség teljes nagyságával.
Az alakváltozási sebességet leíró Cotrell-féle összefüggés
Cotrell H. [4] a makroszkopikus alakváltozási sebesség és a diszlokációk ![]() átlagsebessége között a következő összefüggést írta fel:
átlagsebessége között a következő összefüggést írta fel:
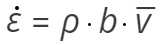
(1)
ahol ![]() – az alakváltozás sebessége, dimenziója sec-1, ρ – a mozgásra képes diszlokációk sűrűsége, dimenziója m-2, b – a mozgásra képes diszlokáció Burgers vektora, dimenziója: m,
– az alakváltozás sebessége, dimenziója sec-1, ρ – a mozgásra képes diszlokációk sűrűsége, dimenziója m-2, b – a mozgásra képes diszlokáció Burgers vektora, dimenziója: m, ![]() – a mozgásra képes diszlokációk átlagsebessége, dimenziója: m/s. A Cottrell-féle (1) összefüggés a 3. ábrában szereplő jellemzők figyelembe vételével értelmezhető.
– a mozgásra képes diszlokációk átlagsebessége, dimenziója: m/s. A Cottrell-féle (1) összefüggés a 3. ábrában szereplő jellemzők figyelembe vételével értelmezhető.
A diszlokációk v átlagsebessége Partin and Findley [5] szerint a kristályra ható τ* tényleges csúsztatófeszültségtől a (2), tapasztalati összefüggés szerint függ,
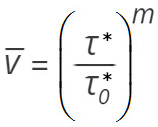
(2)
ahol τ*– a diszlokáció sebességét közvetlenül meghatározó tényleges csúsztatófeszültség, a τ*0 – állandó a v = 1 cm/s diszlokációsebességet okozó tényleges csúsztatófeszültséget reprezentálja Prekel et al, 1968 szerint [6], az m – anyagi paraméter, diszlokáció sebesség–feszültség együttható. Megjegyzés: a (2) egyenlet a ![]() átlagsebességre csak akkor adhat dimenzió szempontjából korrekt eredményt, ha a hatványkitevős tagot még megszorozzuk egy m/s dimenziójú állandó értékkel. A τ*0 tényleges csúsztatófeszültség definíciójából következik, hogy ennek a konstansnak a számszerű értéke 1, hiszen τ* = τ*0 esetében a diszlokáció átlagsebessége egységnyi, azaz 1 m/s.
átlagsebességre csak akkor adhat dimenzió szempontjából korrekt eredményt, ha a hatványkitevős tagot még megszorozzuk egy m/s dimenziójú állandó értékkel. A τ*0 tényleges csúsztatófeszültség definíciójából következik, hogy ennek a konstansnak a számszerű értéke 1, hiszen τ* = τ*0 esetében a diszlokáció átlagsebessége egységnyi, azaz 1 m/s.
Ezek figyelembe vételével a (2) egyenlet dimenzió szempontjából is helyes alakja a következő:
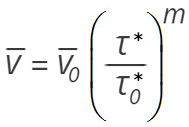
(2.a)
ahol ![]() – konstans, értéke 1m sec-1.
– konstans, értéke 1m sec-1.
Így a Cottrell-féle elméletet megtestesítő összefüggés a következőképpen írható fel:
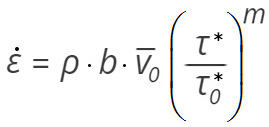
(3)
A Cottrell-féle elméletet megtestesítő (3) egyenlet alapján már elemezhetjük az alakváltozási sebesség és a diszlokáció-sűrűség változásának hatását. Az alakváltozási sebesség változtatásának hatása méréstechnikai szempontból lényeges, hiszen az úgynevezett „strain rate change” vizsgálattal lehet meghatározni az m kitevő értékét, míg a diszlokáció-sűrűség megváltozásának hatása éppen a folyási jelenség értelmezéséhez nyújt segítséget.
I. Az alakváltozási sebesség változásának hatása τ*-ra
Szakítóvizsgálat közben változtassuk meg az alakváltozási sebességet ugrásszerűen ![]() értékről
értékről ![]() értékre, ahol az adott vizsgálattípus esetén ez utóbbi érték általában nagyobb. Mivel az alakváltozási sebesség változtatása szinte időigény nélkül következik be, feltételezzük, hogy a minta anyagának ρ diszlokációsűrűsége nem változik, továbbá, a b Burgers-vektor, a v0 és a τ0* értéke is állandó. Az alakváltozási sebességet írjuk fel a két esetre a (4) egyenlet szerint a (3) egyenlet figyelembe vételével.
értékre, ahol az adott vizsgálattípus esetén ez utóbbi érték általában nagyobb. Mivel az alakváltozási sebesség változtatása szinte időigény nélkül következik be, feltételezzük, hogy a minta anyagának ρ diszlokációsűrűsége nem változik, továbbá, a b Burgers-vektor, a v0 és a τ0* értéke is állandó. Az alakváltozási sebességet írjuk fel a két esetre a (4) egyenlet szerint a (3) egyenlet figyelembe vételével.
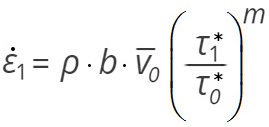
(4a)
illetve
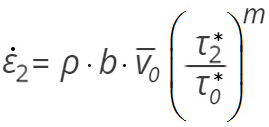
(4b)
Jelöljük az alakváltozási sebesség hányados értékét ![]() -nal, és végezzük el a lehetséges egyszerűsítéseket, akkor τ2*-ra nézve a következő összefüggést kapjuk:
-nal, és végezzük el a lehetséges egyszerűsítéseket, akkor τ2*-ra nézve a következő összefüggést kapjuk:
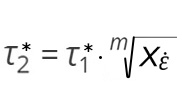
(5)
Mivel a kísérleti eredmények szerint [5] m értéke szobahőmérsékleten 10-es nagyságrendű, belátható, hogy az alakváltozási sebesség változása τ* értékére jelentős, ezt a megállapítást számszerűsítve a következőket mondhatjuk: ha ![]() = 10, és m = 10, akkor a τ* változásának mértéke
= 10, és m = 10, akkor a τ* változásának mértéke ![]() , melynek számszerű értéke: 1,2589, vagyis az effektív feszültség mintegy 25%-kal növekszik.
, melynek számszerű értéke: 1,2589, vagyis az effektív feszültség mintegy 25%-kal növekszik.
II. A mozgásra képes diszlokáció sűrűségének megváltozása
Ennek az esetnek a vizsgálatakor tételezzük fel, hogy az alakváltozási sebesség a diszlokáció-sűrűség megváltozása előtt és utána is állandó marad. Ekkor a (3) egyenlet alapján írhatjuk, hogy
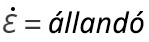
(6a)
és ebből adódik, hogy
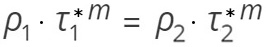
(6b)
ahol megfelelő alsó indexekkel jelöltük a diszlokáció-sűrűség megváltozása előtti és utáni állapotot. Ebben az esetben is a korábbiakhoz hasonlóan állandónak tekintettük a b Burgers-vektort, a v0 sebességet és a τ*0 feszültséget. A diszlokációsűrűség megváltozásának mértékét jelöljük Xρ-val, akkor a τ* megváltozásának mértéke az (5) egyenlethez hasonló (7) egyenlettel írható fel.
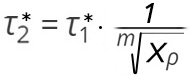
(7)
Ellentétben az alakváltozási sebesség megnövelésével, a mozgásra képes diszlokációk sűrűségének megnövelésekor a τ* értéke nem nő, hanem csökken a (7) egyenlet szerint.
Figyelembe véve a ρ diszlokáció-sűrűség megváltozásának reális és az m kitevő korábban már figyelembe vett értékét, a τ* feszültség értékének csökkenése ebben az esetben a ![]() értékkel, vagyis 1,25-tel való osztással adódik.
értékkel, vagyis 1,25-tel való osztással adódik.
A Lüders nyúlás közbeni feszültségváltozás elemzésekor – ahogy azt már korábban írtam – a (7) egyenletet vesszük alapul.
A külső terhelésből adódó és az effektív feszültség kapcsolata
A diszlokáció sebességét közvetlenül meghatározó tényleges feszültség nagysága szabványos szakítóvizsgálattal közvetlenül nem határozható meg, de a szakítóvizsgálat technikai elrendezése lehetőséget teremt a külső terhelésből adódó feszültségnek belső feszültségre (internal stress) és tényleges feszültségre (effective stress) való felbontására. Ezt a speciális vizsgálatot feszültség-relaxációs vizsgálatnak nevezzük [7]. Ennek lényege az, hogy a szakítás folyamata közben – adott külső feszültségi szinten – megállítjuk a szakítást, és a külső terhelésből adódó feszültség időbeli lefutását követjük.
A relaxációs vizsgálat közben a próbatest és a szakítógép egységes rendszert képez, amelyben a szakítógép erőmérő celláját egy nagy merevségű rugónak tekintjük, melynek rugóállandója E. Nyújtsuk a szakító próbatestet lpróba hosszúságúra, miközben a terhelés F-re növekszik, eközben pedig az erőmérő cella „rugója” l1 hosszúságú lesz. Tételezzük fel továbbá, hogy a relaxációs vizsgálat közben az l1+lpróba állandó, amennyiben a szakítógép állványa nagyon merev. A feszültség-relaxáció közben a próbatest maradó alakváltozást szenved, amelynek nagysága Δlpróba. A terhelés csökkenés értéke értelemszerűen az alábbi kifejezéssel adható meg:
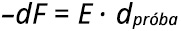
(8)
Ebből a feszültségcsökkenés pedig
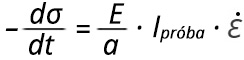
(9)
ahol F – a külső terhelő erő N-ban, a – a próbatest keresztmetszete m2-ben.
A további elemzés szempontjából egy relaxációs vizsgálattal mód van a külső terhelésből adódó feszültségnek a belső és tényleges feszültségre való felbontására, mert megfelelő hosszúságú relaxációs időt választva a próbatest képlékeny alakváltozása megszűnik, ami egyben azt is jelenti, hogy a diszlokációra ható tényleges feszültség nagysága 0-hoz közeli értéket vesz fel. A 4. ábra a megszakított szakítóvizsgálat közben elvégzett feszültség-relaxációs vizsgálat eredményét szemlélteti, amelyen bejelöltük a belső és a tényleges feszültség nagyságát Gupta és Li nyomán [8].
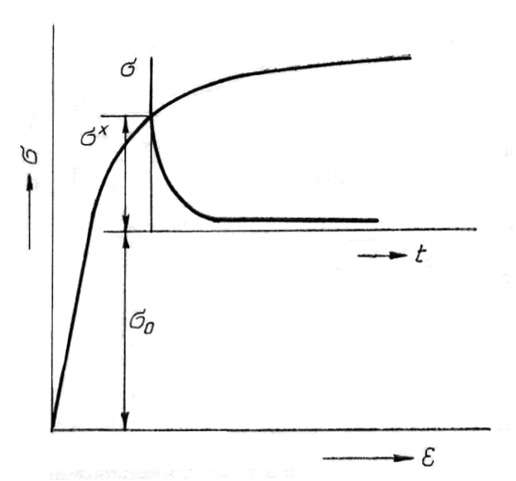
Az elmondottakat a normális és a csúsztatófeszültségekre nézve a (10) és (11) egyenlet fejezi ki.
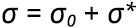
(10)
illetve
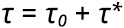
(11)
A feszültség-relaxációs vizsgálattal számos további, a képlékeny alakváltozás szempontjából lényeges adat határozható meg. Ezekre azonban a jelen esettanulmányban nem térünk ki, a feszültség-relaxáció elméletéről és gyakorlatáról egy többszerzős cikkünkben [7] számoltunk be, megjegyezve azt, hogy ez a témakör mind a mai napig a képlékeny alakváltozás mechanizmusával foglalkozó kutatások fókuszában áll.
A munkahipotézis
A szakítóvizsgálat közben annak kezdeti szakaszában a polírozott felületű próbatesteken közvetlenül megfigyelhető jelenségek és terhelés-ingadozások, a képlékeny alakváltozás diszlokációs mechanizmusa, a makroszkópos és a mikroszkópos jelenségek közötti kapcsolatra vonatkozó Cottrell-elmélet alapján a feszültség-relaxációs folyamat elméletéből adódó ismeretek figyelembe vételével a következő munkahipotézis fogalmazható meg az ennek az esettanulmánynak a címében feltett kérdésekkel kapcsolatban:
- A Lüders-nyúlás közbeni terhelésváltozás a működő Lüders-frontok hosszával, pontosabban a mozgásban lévő diszlokációk számának változásával hozható kapcsolatba. Feltételezzük tehát, hogy a mozgó diszlokációk száma egyenesen arányos a működésben lévő Lüders-frontok hosszával.
- A Lüders-nyúlás közbeni terhelésváltozás mértékét a Cottrell-féle elmélet alapján magyarázhatjuk, figyelembe véve azt a feszültség-relaxáció elméletéből levonható megállapítást, miszerint a külső terhelésből adódó feszültség belső feszültségre és tényleges feszültségre bontható.
A vizsgált jelenségekre vonatkozó ismeretek szintézise
Ahogy azt már a jelenség leírásakor is említettem, a saját megfigyeléseimet és megállapításaimat egy, az adott témáról szóló elemzéssel [3] összevetve ismertetem. A jobb követhetőség kedvéért ez utóbbi elemzés eredeti német nyelvű, és az általam magyarra fordított változata ezen a linken olvasható (új ablakban nyílik meg). Az eredeti elemzéshez fűzött megjegyzéseimet a magyar nyelvű fordításba illesztettem be, a fordított szövegrészeket kurziválással különítettem el a saját szövegemtől.
A mikro képlékeny tartományból az általános folyásba való átmenet folytonosan vagy nem folytonosan egyaránt végbemehet. Az utóbbi esetben a feszültség–nyúlás diagramon a Hooke-féle egyeneshez csatlakozóan többé-kevésbé jelentős bizonytalanság lép fel (felső folyási határ).
Ha jól értettem az „Unstätigkeit” fogalmat, akkor a [3] szerzője valószínűleg arra utalt a felső folyási határ nagyságával kapcsolatban, hogy az még párhuzamos mintákon mérve is szélsőségesen változhat. Ennek alapvető oka az, hogy a szakítógépek szokásos befogó fejei nem biztosítják az egytengelyű húzó igénybevétel feltételeit, és maga a szakítópróbatest kialakítása sem előnyös ilyen szempontból. A Mucsi A. [9] által kifejlesztett, egytengelyűséget biztosító befogó fejjel végzett vizsgálatok egyértelműen bizonyították a hagyományos befogó fejek meghatározó szerepét. Arra a meglepő eredményre jutott, hogy a lágyacélok felső folyási határa még a szakítószilárdságot is meghaladhatja. Az utóbbi állítást igazoló szakítódiagram részlet az 5. ábrán látható.
Az ezzel együtt járó εL nyúlást Lüders nyúlásnak nevezzük. Eközben egy majdnem homogén alakított tartomány jön létre (Lüders sáv), és a képlékeny alakváltozás a nem alakított tartományba hatol be (ez az eltérő fényvisszaverődés miatt folyási alakzatként válik láthatóvá).
Kísérleteim során szintén a reflexiós képesség megváltozása miatt követhettem a Lüders tartományok kialakulását és az alakított és nem alakított tartományok határvonalának mozgását. Hasonló megfigyeléseket tehettem azonban a vékony oxidréteggel fedett próbatestek szakítása közben is, ez utóbbi lehetőség sokkal egyszerűbben megvalósítható, a próbatest felületét ugyanis nem kell polírozni.
Az inhomogén alakváltozás a hideghengerléssel végzett lemezalakításkor vagy mélyhúzáskor nem kívánt jelenségnek tekinthető, amely megnövekedett felületi érdességhez vezet. Mivel a folyási vonalak ismét eltűnnek amikor is a Lüders sávok a teljes tartományra már kiterjedtek, a lemezalakításkor arra kell törekedni, hogy az alakítás mértéke a Lüders nyúlás mértékét meghaladja. A Lüders sávok kiszélesedésének befejeződése után az alakváltozás makroszkóposan nézve homogén lesz, és az alakítási szilárdság ismét növekedni kezd.
Ezek a megállapítások lényegében helyesek, de a lágyacél lemezek feldolgozásakor kizárólag dresszírozott állapotú lemezeket használnak, amelyek alakítása közben már nem alakulnak ki makroszkópos Lüders tartományok. Értelemszerűen, ha a lemezalakítás közben közbenső lágyításra van szükség, akkor a német szövegben említett, kedvezőtlen jelenségekre számítani kell.
A felső folyáshatár megjelenése alapvetően az alakváltozást okozó diszlokációk és az idegen atomok közötti rugalmas kölcsönhatásra vezethető vissza. Cottrell feltevése szerint ebben a folyamatban főleg az éldiszlokációk és az intersztíciósan oldott atomok szerepe a meghatározó, amelyek a diszlokációk tágult tartományában helyezkednek el. Így az intersztíciós atomok Cottrell felhőket alkotnak, amelyek mozgása a rács torzulási energiájának csökkenése miatt gátolt. Csak a külső feszültség megnövekedése révén szabadulhatnak meg a diszlokációk az intersztíciós atomok alkotta felhőktől. Eközben a diszlokációk megsokszorozódnak, ami azt jelenti, hogy számos mozgásra képes diszlokáció képződik, mégpedig olyanok, amelyeknek a szabad úthossza viszonylag nagy.
A fenti szövegrész a felső folyási határnál lezajló folyamatok klasszikus, Cottrell-féle megközelítését foglalja össze. Mai ismereteink szerint azonban ez az elmélet számos további kérdés tisztázását igényli. Ismert például, hogy a diszlokáció vonala vagy szemcsehatáron végződhet, vagy önmagában zárulhat hurkot képezve. Mivel a Cottrell-féle elmélet csak az éldiszlokációk tágult tartományainak az intersztíciós atomokkal való kölcsönhatását nevezi meg okként, kérdéses, hogy egy zárt diszlokációhurok esetén ezek az atomok a hurok melyik részén helyezkednek el, illetve hogyan gátolják a hurok mozgását. A mozgásra képes diszlokációk számának megsokszorozódására nem csak ezeknek az oldott atomok felhőitől való megszabadulása révén van lehetőség, hanem Li és Chou [10] szerint a szemcsehatárban lévő lépcsők is képesek ilyen diszlokációkat kibocsátani. Az elmélet lényegét az alábbiakban lehet összefoglalni:
A Hall-Patch összefüggést le lehet vezetni a Frank-Read források működése eredményeképpen kialakuló diszlokáció-felsorakozás alapján, vagy J.C.M. Li javaslata szerint, mégpedig a szemcsehatár-lépcsőkből származó erdő-diszlokációk okozta szilárdságnövekedés alapján. A diszlokáció-forrásként működő lépcsők (ledges) kialakulásának folyamatát szemlélteti a 6. ábra vázlatsorozata. A diszlokációknak egy speciális nagyszögű határban való megjelenése okozta változásokat az [1] irodalomban található magyarázat alapján értelmezhetjük. Az, hogy a két említett mechanizmus közül melyik működik, mind a mai napig nincs kísérletileg eldöntve.
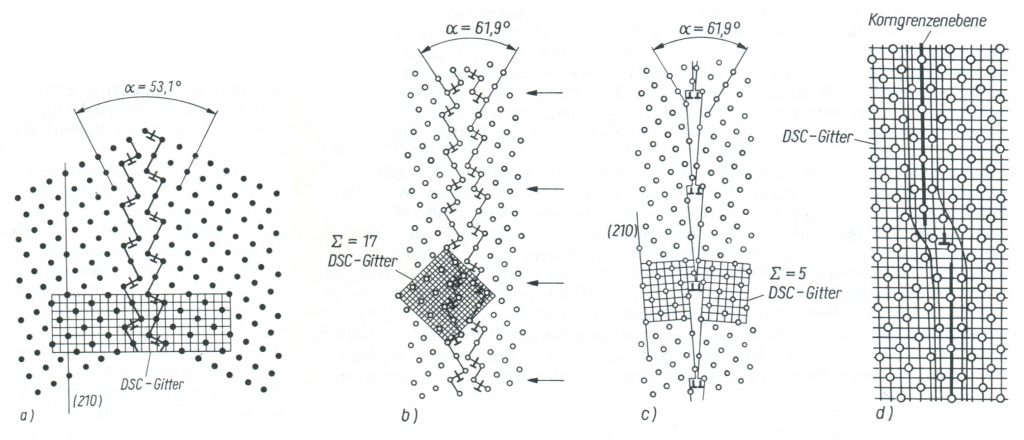
Valóban nagyon meglepő, hogy a diszlokáció-felsorakozás egyszerű elrendeződése nem elegendő a folyás jelenségének megértéséhez. A nem-felsorakozási modellek hiányoznak. Ezek között az alakítási keményedési modellek igénylik a diszlokációsűrűség–alakváltozás közötti kapcsolatot leíró összefüggést, amely azonban csak bizonyos rendszerekre nézve érvényes. Ezek nem adnak megoldást a Lüders féle alakváltozásra, továbbá, a szemcsehatár szerkezetének hatásával kapcsolatban sem. A szemcsehatár forrásmodellek elkerülik ezeket a nehézségeket a szemcsehatárban lévő források koncepciójának bevezetésével. Bár számos megfigyelés létezik a szemcsehatárokban lévő kiugrásokra, lépcsőkre nézve, amelyekből a szemcsehatár diszlokációkat bocsájt ki. Ez azonban nem szolgáltat közvetlen bizonyítékot arra nézve, hogy ezek száma a hőkezelés, nyomás és besugárzás hatására megváltozhat, a források sűrűségének közvetlen meghatározása a szemcsehatárban mind a mai napig hiányzik. A szemcsehatárból kibocsájtott diszlokációk egymással kölcsönhatásba lépnek, és a rájuk ható tényleges feszültségnek megfelelő sebességgel mozognak. Ahhoz, hogy a Lüders front sebességét és ennek az alakváltozási profilját meghatározó tényezőit megértsük, diszlokáció dinamikai elemzésre van szükségünk. Az ilyen irányú elemzések szükségesek ahhoz, hogy fényt derítsünk a folyási jelenség mechanizmusának részleteire.
Úgy gondolom, hogy akár kísérletileg is el lehetne dönteni, hogy a Cottrell-től illetve a Li és társától származó elméletek közül melyik írja le helyesebben a felső folyási határon elinduló folyamatokat. Ha összehasonlítanánk a folyás előtti és a megfolyt anyag diszlokáció-sűrűségét, akkor erre a kérdésre választ kaphatnánk. Röntgen-diffrakciós vagy vékony fémfóliás transzmissziós elektronmikroszkópos vizsgálat egyaránt szóba jöhet. Érdekes lehetne azt is megvizsgálni, hogy a szabaddá vált diszlokációk által „elhagyott” intersztíciós atomoknak mi lesz a sorsa, erre a kérdésre talán a termoelektromos erő mérésével kaphatunk választ.
A képlékeny alakváltozás sebességét ![]() egy húzással igénybevett szerkezeti anyagban a következő egyenlet fejezi ki:
egy húzással igénybevett szerkezeti anyagban a következő egyenlet fejezi ki:
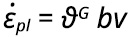
ahol ϑG – a mozgásra képes diszlokációk száma, b – a Burgers vektor, v – a diszlokációk átlagos mozgási sebessége.
Véleményem szerint a [3] irodalomban szereplő idézett fenti képlet abban a pillanatban írja le helyesen illetve értelmezhető módon az alakváltozási sebességnek a diszlokáció-sűrűségtől és a mozgásra képes diszlokációk sebességétől való függését, amikor a próbatest befogása és a mérőhossz közötti íves átmeneti tartományban elindul egy Lüders tartomány kialakulása, majd ez a próbatest mérő hossza felé kiszélesedik, miközben a Lüders tartomány másik határoló vonala a próbatest szélességének növekedése miatt megáll. Ekkor joggal feltételezhetjük, hogy az alakváltozás egyetlen Lüders frontra koncentrálódik, vagyis a figyelembe veendő diszlokációk száma a Lüders front hosszával arányos. A Hill féle képlékenységtan szerint a Lüders front vonala a szakítópróbatest tengelyével 45o-nál nagyobb, 50o körüli szöget zár be.
A diszlokációk átlagos sebessége az anyagra ható húzófeszültség nagyságával arányos, és egy állandó adott alakváltozási sebesség esetén a ϑG diszlokációsűrűség növekedésekor a v diszlokáció sebesség csökkenéséhez vezet, ami egy hirtelen feszültség-esésben mutatkozik meg.
Ebben a hosszú mondatban az első állítás, miszerint „a diszlokációk átlagos sebessége az anyagra ható húzófeszültség nagyságával arányos”, véleményem szerint hibás, hiszen ellentmond Partin and Findley [5] kísérletileg alátámasztott, és azóta számtalanszor igazolt eredményének. Bár az eredeti szövegben nem egészen világos az, hogy az általam hibásnak ítélt állítás a folyamat melyik részére vonatkozik, de ennek az állításnak a helytállósága a felső folyási határra vonatkozóan vagy akár a folyási nyúlás közbeni jelenségekre vonatkoztatva egyaránt megkérdőjelezhető.
A folyási nyúlás közbeni jelenségek, nevezetesen feszültségingadozások értelmezésekor, amint azt a következő meggondolások igazolni fogják, a diszlokáció-sebességnek a húzófeszültségtől való függésének leírásakor hatványkitevős összefüggést kell figyelembe vennünk. Induljunk ki a már korábban tárgyalt helyzetből, amikor egyetlen Lüders front hatol be a még alakítatlan anyagba. Vegyük figyelembe a τ* tényleges feszültség és a diszlokáció-sűrűség közötti (7) egyenletet, továbbá azt a körülményt, hogy a feszültség-relaxációs elmélet szerint a tényleges feszültség – legyen az csúsztató vagy normális feszültség – a mindenkori külső feszültség és a belső feszültség különbsége (lásd a (10) egyenletet). A két összefüggés segítségével írjuk fel a második Lüders tartomány kialakulásával létrejövő helyzetet. Így írható, hogy
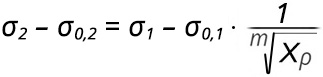
(12)
A (12) egyenletben a 2 alsó index minden esetben az új Lüders tartomány kialakulása utáni helyzetre vonatkozik. A (12) egyenletből fejezzük ki a σ2 külső feszültséget annak figyelembe vételével, hogy a σ0,i (ahol i = 1 vagy 2) belső feszültségeket a külső feszültség Xσ2 illetve Xσ1-szereseként definiáljuk a feszültség-relaxációs elmélet szerint. Az Xσ2 illetve Xσ1 értéke értelemszerűen 1-nél kisebb érték. Vegyük továbbá azt is figyelembe, hogy a (12) egyenletben a diszlokáció-sűrűség megváltozásának Xρ –t a munkahipotézis szerint a Lüders frontok hosszának megváltozását kifejező arányszámmal kell helyettesíteni. Ezt az értéket XL –nek nevezzük. Mindezek figyelembe vételével σ2-re a következő egyenlet adódik:
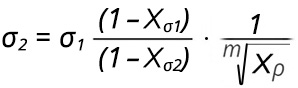
(13)
A (13) egyenlet alapján három eset különböztethető meg, nevezetesen:
- Ha (1–Xσ2) =(1–Xσ1). Ekkor a σ2 ugyanolyan mértékben változik a σ1-hez képest, mint amit a (7) egyenlet az effektív feszültségekre adott meg. Más szavakkal ez azt jelenti, hogy a σ0 belső és a σ külső feszültség aránya nem módosul az újabb Lüders tartomány kialakulásakor.
- Ha (1–Xσ2)>(1–Xσ1), akkor a (13) képletben szereplő tört értéke 1-nél kisebb, vagyis a belső feszültség és a külső feszültség arányának ilyen irányú megváltozása a σ2 külső feszültség további csökkenését jelenti. Ez megegyezik azzal az állítással, miszerint σ2 a σ1-hez képest erősebben csökken, mint amit a Lüders frontok hosszának megváltozása okozna.
- Amennyiben az (1–Xσ2)< (1–Xσ1), akkor a (13) egyenletben szereplő tört értéke 1-nél nagyobb lesz, és az előbbiek szerinti gondolatmenetet követve, a σ2 külső feszültség a σ1 külső feszültséghez viszonyítva kevésbé változik, mint amit a Lüders frontok hosszának megváltozása okozna.
Ebből az elemzésből az is következik, hogy alapvető kérdésként merül fel, hogy a σ0 értéke állandó marad-e a folyási nyúlás közben. Amennyiben ez kísérletileg igazolható, akkor valószínű, hogy az újabb Lüders front megindulása utáni helyzetben a σ* tényleges feszültség lecsökkenése miatt az Xσ2 arányszám növekszik, vagyis a valóságban a harmadikként tárgyalt eset tükrözi a realitást.
Kis alakváltozások esetén
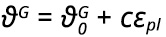
ahol ![]() – az alakítatlan állapotú anyagban jelenlévő mozgásra képes diszlokációk száma, c – állandó.
– az alakítatlan állapotú anyagban jelenlévő mozgásra képes diszlokációk száma, c – állandó.
Ugrásszerű feszültségesés mindig akkor lép fel, ha ![]() kicsi, ami például színvas esetében a diszlokációknak az intersztíciósan oldott karbon és nitrogénatomok alkotta Cottrell felhők általi blokkolása miatt állhat elő.
kicsi, ami például színvas esetében a diszlokációknak az intersztíciósan oldott karbon és nitrogénatomok alkotta Cottrell felhők általi blokkolása miatt állhat elő.
Ez a megállapítás nehezen értelmezhető, mert nem egyértelmű, hogy a szövegben mit jelent a „kis alakváltozás” fogalma.
A munkahipotézis tételeinek elfogadása vagy elvetése
Amennyiben a Lüders frontok mozgásával kapcsolatban lévő kísérleti és elméleti eredményekre alapozott szintézisben foglaltak megállják a helyüket, akkor a munkahipotézis két állítására egyértelműen választ kell tudnunk adni. A munkahipotézisekre azonban az is jellemző, hogy az azokra keresett válasz újabb értelmes kérdéseket vet fel, amelyek a kérdés végleges megválaszolásához is elvezethetnek. Amint látni fogjuk, az adott esetben is ez a helyzet a jellemző.
A munkahipotézis első pontjában azt állítottuk, hogy a folyási nyúlás közbeni feszültségváltozás a mozgásban lévő Lüders frontok hosszával, és így a mozgó diszlokációk számával van összefüggésben. Ez az állítás a Cottrell féle elmélet szerint belátható, de – ahogy az előbb említettem – újabb kérdések merülnek fel. Egyrészt kísérleti úton tisztázni kellene, hogy a folyási nyúlás közben valójában csak a Lüders frontban van diszlokáció-mozgás. Ez más szavakkal annak tisztázását igényli, hogy a már megfolyt, úgynevezett Lüders tartományokon belül nincs alakváltozás, az alakváltozás csak a határvonal környékére terjed ki. Az is kérdés, hogy a felső folyási határnál lényegesen kisebb feszültségszinten bekövetkező Lüders nyúlás során hogyan képesek az intersztíciós atomokkal blokkolt diszlokációk ismét szabaddá válni. Kísérletileg az is vizsgálandó lenne, hogy egy újabb Lüders tartomány megjelenésekor a már korábban kialakult tartományok határvonalainak elmozdulási sebessége hogyan változik.
Úgy gondolom, hogy a felvetett kérdésekre a video-érzékelőkkel ellátott korszerű szakítógépek alkalmasak, különösen akkor, ha a szakító próbatestet megfelelő felbontású Marker-jelekkel látjuk el.
A munkahipotézis második tételére, amely a Lüders nyúlás közbeni feszültség-változás mértékére vonatkozik, már jó számszerű közelítést adhatunk. Viszonylag egyszerűbb a helyzet a négyzetgyökös tagra nézve, hiszen egy újabb Lüders tartomány kialakulásával a mozgásban lévő Lüders frontok száma egyről háromra nő, vagyis az m-dik gyök alatt 3 szerepel. Az m értékére nézve már megadtuk, hogy az 101 nagyságrendű, m értéke egy adott acélminőség esetén „strain rate change” vizsgálattal, vagy feszültség-relaxációs kísérlettel egyaránt meghatározható. Fenti meggondolások szerint az m-dik gyökös tag értéke 1,116, ami kb. 10%-os külső feszültség-csökkenést testesít meg. Amennyiben egyszerre több Lüders tartomány alakul ki, akkor a feszültség-csökkenés mértékére nézve az 1. táblázatban szereplő adatok irányadóak.
| XL | 2 | 3 | 4 | 5 | 10 |
| 1,071 | 1,1161 | 1,148 | 1,1746 | 1,2589 |
ha m=10, és XL értéke 2, 3, 4…
A (13) összefüggés kapcsán három esetet különböztettünk meg, és azt valószínűsítettük, hogy a harmadik eset tükrözi a valós helyzetet, vagyis ha (1-Xσ2)< (1-Xσ1). Ez, amint azt már megállapítottuk, azt jelenti, hogy a belső feszültség és a tényleges feszültség egymáshoz való viszonyának várható megváltozása a Lüders frontok hosszának megváltozásával szemben hat.
Ahhoz, hogy az (1-Xσi) számértékét megbecsüljük, egy lágyacélon végzett feszültség-relaxációs vizsgálatból származó, és a 6. ábrán látható diagramot hívjuk segítségül.
![7. ábra. Egy lágyacél mintán felvett feszültség-relaxációs vizsgálat eredménye [7] nyomán.](https://www.anyagtudomany.eu/wp-content/uploads/2021/12/luders-7.jpg)
A 7. ábrából leolvasható, hogy a szakítóvizsgálat megállításának pillanatában a terhelő erő 3200N-ról indul, és viszonylag rövid idő alatt 2800N-ra esik. Ezeknek az adatoknak alapján az Xσi értéke 2800/3200=0,875, vagyis az (1- Xσi) értéke 0,125. Az (1-Xσ1)/ (1-Xσ2) tört értéke feltehetően 0,120 és 0,130 körüli számok hányadosát jelentheti, ami – ha a szélső értékeket vesszük figyelembe – 0,92-vel egyenlő. Ez az érték azt jelzi, hogy a σ0 és a σ arányának változása viszonylag érzékenyen befolyásolja a Lüders front hosszának megváltozásából adódó feszültség-csökkenést. Ezeket a közelítéseket kísérleti úton jól lehet ellenőrizni, ha a Lüders nyúlás közben feszültség-relaxációs vizsgálatokat végzünk a σ0/σ reális arányának meghatározására.
Az eredmények validálása
A Lüders nyúlás közbeni feszültség-változásra nézve az elméleti megfontolások alapján becslést adhatunk. Ehhez azonban ismerni kell a kísérleti anyagra érvényes m kitevő értékét, és például feszültség-relaxációs vizsgálattal meg kell határozni a belső feszültség/külső feszültség arányát. Ezek a vizsgálatok a korszerű, nagy merevségű mechanikus szakító berendezéseken végrehajthatók.
Úgy gondolom, hogy akkor sem kell kétségbe esni, ha a kísérleti eredmények az elmélet alapján becsült értékeket rosszul közelítik, mert ez a helyzet új elmélet megfontolásokhoz is elvezethet.
Irodalom
[1] Schatt, Werner: Einführung in die Werkstoffwissenschaft. Deutscher Verlag für Grundstoffindustrie, Leipzig. 7. überarbeitete Auflage, 1991. 344-345.
[2] Clement A. – Tóth J. – Verő B.: A szakítódiagram kezdeti szakaszának fémtani – képlékenységtani elemzése lágyacélok esetén. BKL Kohászat 106: (11) pp. 496-503. (1973)
[3] Schatt, Werner – Hatrmut, Worch: Werkstroffwissenschaft. Deutscher Verlag für Grudstoffindustrie Stuttgart 1996, p. 381.
[4] Cottrell, H.: 1949. Progress in Metal Physics, Theory of Dislocations. Vol 1.
[5] Partin, K. – Findley, K. O. – Van Tyne, C. J.: 2010. Microstructural and alloy influence on he low-tempereture strengthening behavior of commercial steels used as plates. Materials Science and Engineering A Vol. 527 p. 5143
[6] Prekel, H. L. – Lawley, A. – Conrad, H.: 1968. Dislocation Verocity Measurements in High Purity Molybdenum. Acta Metallurgica, Vol 16.
[7] Verő B.- Fauszt A.- Marczis L.- Horváth Á.: A feszültségrelaxáció elmélete és gyakorlata. BKL Kohászat, 118. évf. 10. szám, 438-443. oldal
[8] Gupta, I.- Li, J. C. M.: Stress Relaxation, Internal Stress, and Work Hardening in some Bcc Metals and Alloys. Metallurgical Transactions vol. 1. August 1970-2323
[9] Mucsi, A.: Effect of gripping system ont he measured upper yield strength estimated by tensile tests, Measurement, Volume 46, Issue 5, June 2013, Pages 1663-1670
[10] Li, J. C. M. – Chou, T.: The Role of Dislocations in the Flow Stress Grain Size Relationships Metallurgical Transactions Volume 1. May 1970 – 1145